Neural Likelihoods via Cumulative Distribution Functions

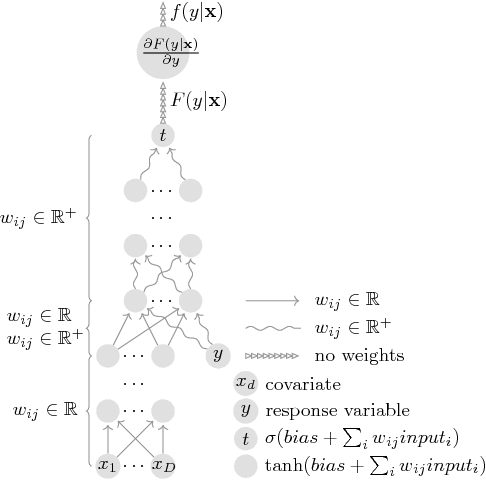
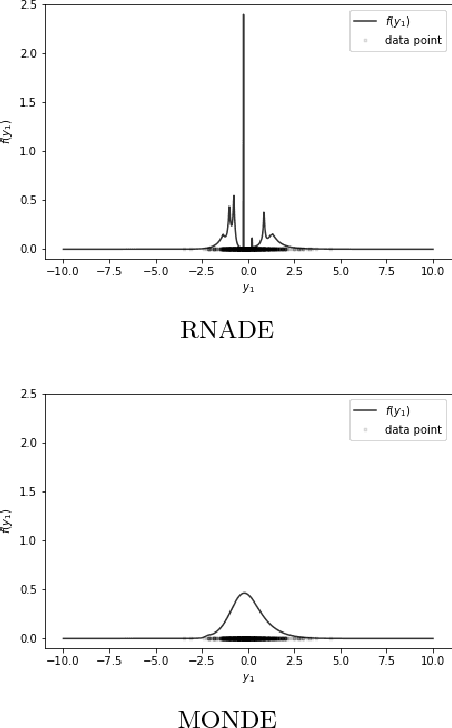
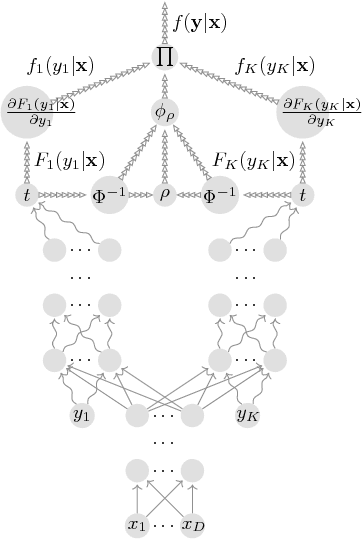
We leverage neural networks as universal approximators of monotonic functions to build a parameterization of conditional cumulative distribution functions. By a modification of backpropagation as applied both to parameters and outputs, we show that we are able to build black box density estimators which are competitive against recently proposed models, while avoiding assumptions concerning the base distribution in a mixture model. That is, it makes no use of parametric models as building blocks. This approach removes some undesirable degrees of freedom on the design on neural networks for flexible conditional density estimation, while implementation can be easily accomplished by standard algorithms readily available in popular neural network toolboxes.