A Variational Latent Equilibrium for Learning in Neuronal Circuits

Brains remain unrivaled in their ability to recognize and generate complex spatiotemporal patterns. While AI is able to reproduce some of these capabilities, deep learning algorithms remain largely at odds with our current understanding of brain circuitry and dynamics. This is prominently the case for backpropagation through time (BPTT), the go-to algorithm for learning complex temporal dependencies. In this work we propose a general formalism to approximate BPTT in a controlled, biologically plausible manner. Our approach builds on, unifies and extends several previous approaches to local, time-continuous, phase-free spatiotemporal credit assignment based on principles of energy conservation and extremal action. Our starting point is a prospective energy function of neuronal states, from which we calculate real-time error dynamics for time-continuous neuronal networks. In the general case, this provides a simple and straightforward derivation of the adjoint method result for neuronal networks, the time-continuous equivalent to BPTT. With a few modifications, we can turn this into a fully local (in space and time) set of equations for neuron and synapse dynamics. Our theory provides a rigorous framework for spatiotemporal deep learning in the brain, while simultaneously suggesting a blueprint for physical circuits capable of carrying out these computations. These results reframe and extend the recently proposed Generalized Latent Equilibrium (GLE) model.

Backpropagation through space, time, and the brain

Effective learning in neuronal networks requires the adaptation of individual synapses given their relative contribution to solving a task. However, physical neuronal systems -- whether biological or artificial -- are constrained by spatio-temporal locality. How such networks can perform efficient credit assignment, remains, to a large extent, an open question. In Machine Learning, the answer is almost universally given by the error backpropagation algorithm, through both space (BP) and time (BPTT). However, BP(TT) is well-known to rely on biologically implausible assumptions, in particular with respect to spatiotemporal (non-)locality, while forward-propagation models such as real-time recurrent learning (RTRL) suffer from prohibitive memory constraints. We introduce Generalized Latent Equilibrium (GLE), a computational framework for fully local spatio-temporal credit assignment in physical, dynamical networks of neurons. We start by defining an energy based on neuron-local mismatches, from which we derive both neuronal dynamics via stationarity and parameter dynamics via gradient descent. The resulting dynamics can be interpreted as a real-time, biologically plausible approximation of BPTT in deep cortical networks with continuous-time neuronal dynamics and continuously active, local synaptic plasticity. In particular, GLE exploits the ability of biological neurons to phase-shift their output rate with respect to their membrane potential, which is essential in both directions of information propagation. For the forward computation, it enables the mapping of time-continuous inputs to neuronal space, performing an effective spatiotemporal convolution. For the backward computation, it permits the temporal inversion of feedback signals, which consequently approximate the adjoint states necessary for useful parameter updates.

Latent Equilibrium: A unified learning theory for arbitrarily fast computation with arbitrarily slow neurons

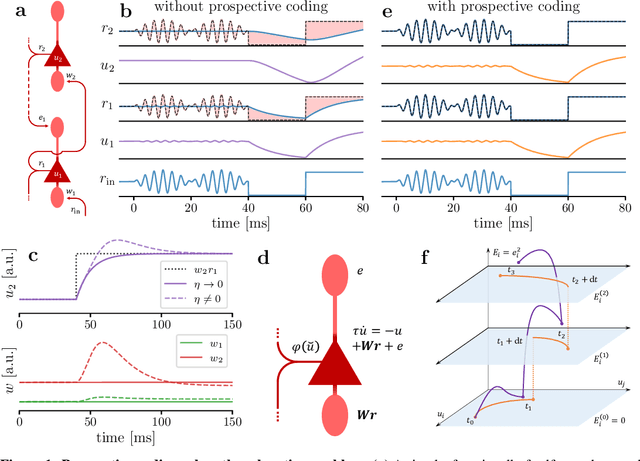
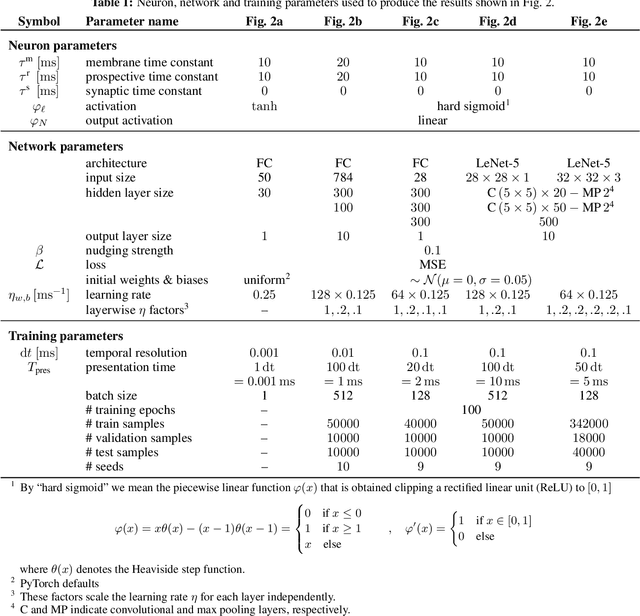
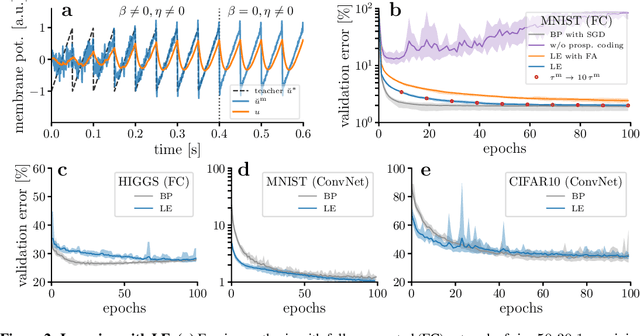
The response time of physical computational elements is finite, and neurons are no exception. In hierarchical models of cortical networks each layer thus introduces a response lag. This inherent property of physical dynamical systems results in delayed processing of stimuli and causes a timing mismatch between network output and instructive signals, thus afflicting not only inference, but also learning. We introduce Latent Equilibrium, a new framework for inference and learning in networks of slow components which avoids these issues by harnessing the ability of biological neurons to phase-advance their output with respect to their membrane potential. This principle enables quasi-instantaneous inference independent of network depth and avoids the need for phased plasticity or computationally expensive network relaxation phases. We jointly derive disentangled neuron and synapse dynamics from a prospective energy function that depends on a network's generalized position and momentum. The resulting model can be interpreted as a biologically plausible approximation of error backpropagation in deep cortical networks with continuous-time, leaky neuronal dynamics and continuously active, local plasticity. We demonstrate successful learning of standard benchmark datasets, achieving competitive performance using both fully-connected and convolutional architectures, and show how our principle can be applied to detailed models of cortical microcircuitry. Furthermore, we study the robustness of our model to spatio-temporal substrate imperfections to demonstrate its feasibility for physical realization, be it in vivo or in silico.