Profiling quantum circuits for their efficient execution on single- and multi-core architectures

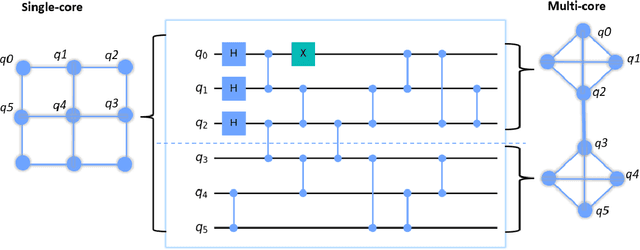
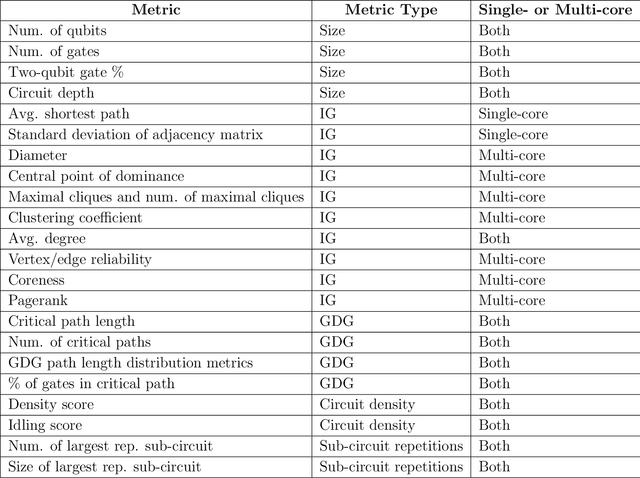
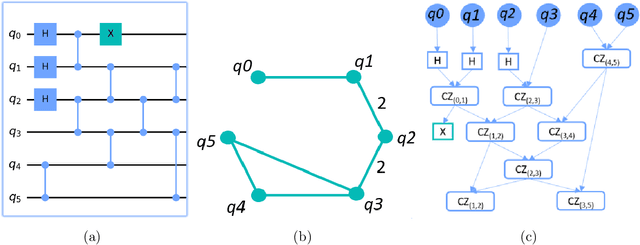
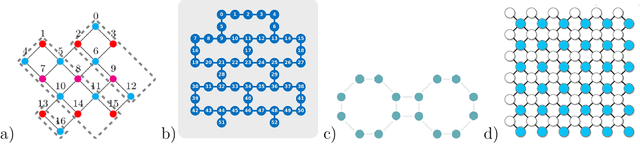
Application-specific quantum computers offer the most efficient means to tackle problems intractable by classical computers. Realizing these architectures necessitates a deep understanding of quantum circuit properties and their relationship to execution outcomes on quantum devices. Our study aims to perform for the first time a rigorous examination of quantum circuits by introducing graph theory-based metrics extracted from their qubit interaction graph and gate dependency graph alongside conventional parameters describing the circuit itself. This methodology facilitates a comprehensive analysis and clustering of quantum circuits. Furthermore, it uncovers a connection between parameters rooted in both qubit interaction and gate dependency graphs, and the performance metrics for quantum circuit mapping, across a range of established quantum device and mapping configurations. Among the various device configurations, we particularly emphasize modular (i.e., multi-core) quantum computing architectures due to their high potential as a viable solution for quantum device scalability. This thorough analysis will help us to: i) identify key attributes of quantum circuits that affect the quantum circuit mapping performance metrics; ii) predict the performance on a specific chip for similar circuit structures; iii) determine preferable combinations of mapping techniques and hardware setups for specific circuits; and iv) define representative benchmark sets by clustering similarly structured circuits.

Circuit Partitioning for Multi-Core Quantum Architectures with Deep Reinforcement Learning

Quantum computing holds immense potential for solving classically intractable problems by leveraging the unique properties of quantum mechanics. The scalability of quantum architectures remains a significant challenge. Multi-core quantum architectures are proposed to solve the scalability problem, arising a new set of challenges in hardware, communications and compilation, among others. One of these challenges is to adapt a quantum algorithm to fit within the different cores of the quantum computer. This paper presents a novel approach for circuit partitioning using Deep Reinforcement Learning, contributing to the advancement of both quantum computing and graph partitioning. This work is the first step in integrating Deep Reinforcement Learning techniques into Quantum Circuit Mapping, opening the door to a new paradigm of solutions to such problems.