Patrick O'Hara
Decision Making under Model Misspecification: DRO with Robust Bayesian Ambiguity Sets
May 06, 2025Abstract:Distributionally Robust Optimisation (DRO) protects risk-averse decision-makers by considering the worst-case risk within an ambiguity set of distributions based on the empirical distribution or a model. To further guard against finite, noisy data, model-based approaches admit Bayesian formulations that propagate uncertainty from the posterior to the decision-making problem. However, when the model is misspecified, the decision maker must stretch the ambiguity set to contain the data-generating process (DGP), leading to overly conservative decisions. We address this challenge by introducing DRO with Robust, to model misspecification, Bayesian Ambiguity Sets (DRO-RoBAS). These are Maximum Mean Discrepancy ambiguity sets centred at a robust posterior predictive distribution that incorporates beliefs about the DGP. We show that the resulting optimisation problem obtains a dual formulation in the Reproducing Kernel Hilbert Space and we give probabilistic guarantees on the tolerance level of the ambiguity set. Our method outperforms other Bayesian and empirical DRO approaches in out-of-sample performance on the Newsvendor and Portfolio problems with various cases of model misspecification.
Decision Making under the Exponential Family: Distributionally Robust Optimisation with Bayesian Ambiguity Sets
Nov 25, 2024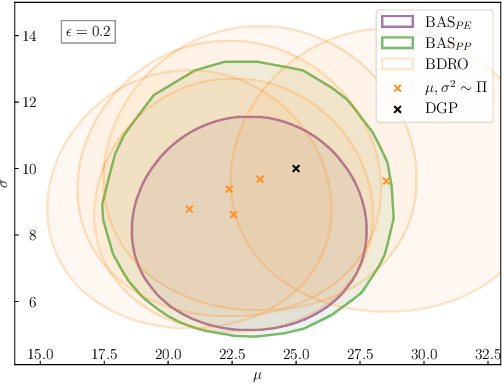
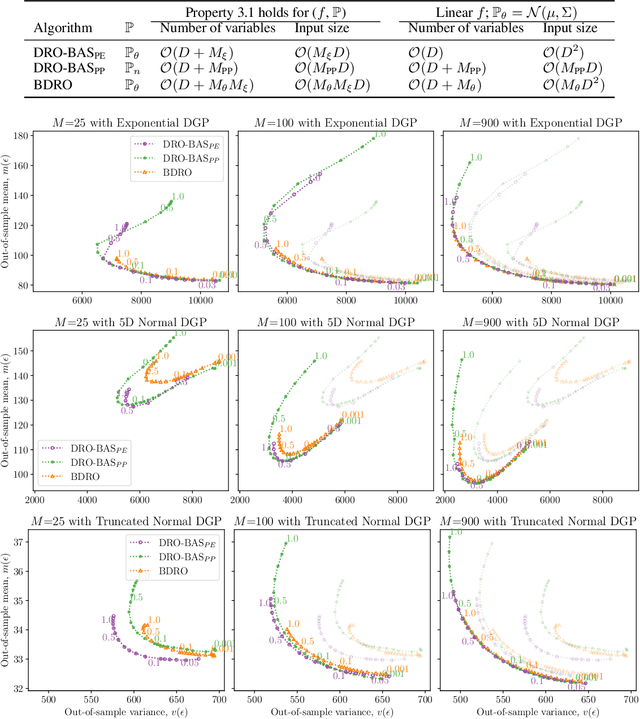

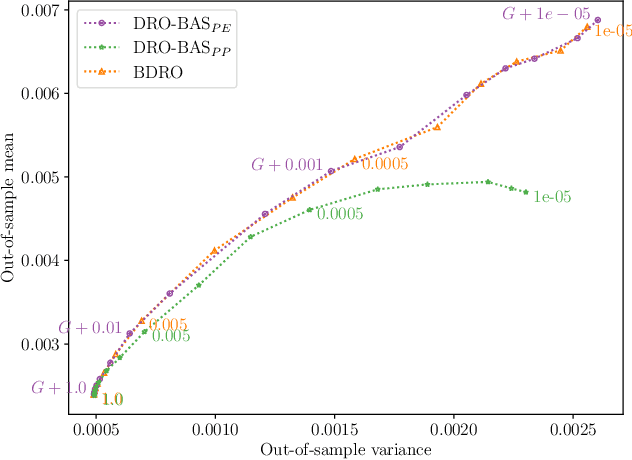
Abstract:Decision making under uncertainty is challenging as the data-generating process (DGP) is often unknown. Bayesian inference proceeds by estimating the DGP through posterior beliefs on the model's parameters. However, minimising the expected risk under these beliefs can lead to suboptimal decisions due to model uncertainty or limited, noisy observations. To address this, we introduce Distributionally Robust Optimisation with Bayesian Ambiguity Sets (DRO-BAS) which hedges against model uncertainty by optimising the worst-case risk over a posterior-informed ambiguity set. We provide two such sets, based on posterior expectations (DRO-BAS(PE)) or posterior predictives (DRO-BAS(PP)) and prove that both admit, under conditions, strong dual formulations leading to efficient single-stage stochastic programs which are solved with a sample average approximation. For DRO-BAS(PE) this covers all conjugate exponential family members while for DRO-BAS(PP) this is shown under conditions on the predictive's moment generating function. Our DRO-BAS formulations Pareto dominate existing Bayesian DRO on the Newsvendor problem and achieve faster solve times with comparable robustness on the Portfolio problem.
Distributionally Robust Optimisation with Bayesian Ambiguity Sets
Sep 05, 2024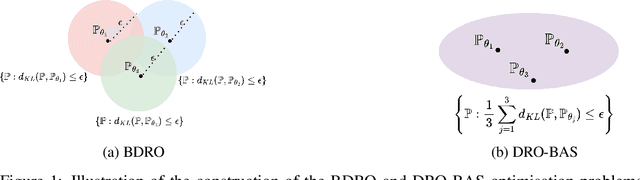
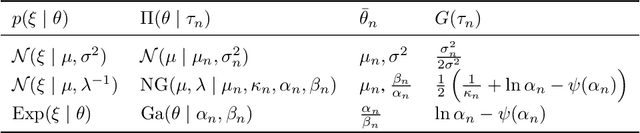
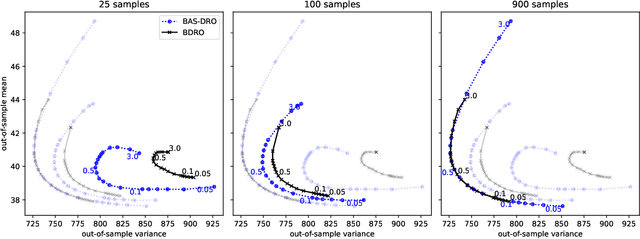
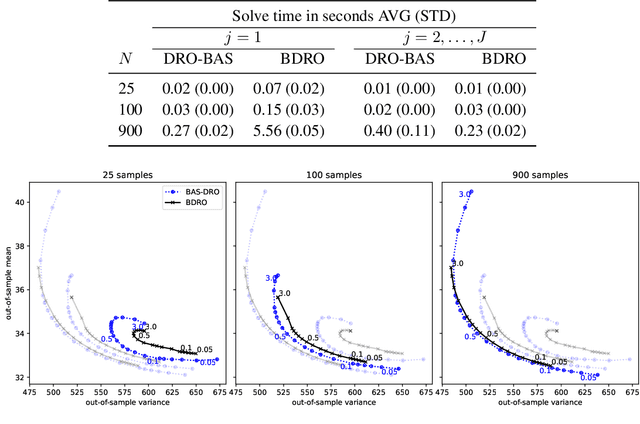
Abstract:Decision making under uncertainty is challenging since the data-generating process (DGP) is often unknown. Bayesian inference proceeds by estimating the DGP through posterior beliefs about the model's parameters. However, minimising the expected risk under these posterior beliefs can lead to sub-optimal decisions due to model uncertainty or limited, noisy observations. To address this, we introduce Distributionally Robust Optimisation with Bayesian Ambiguity Sets (DRO-BAS) which hedges against uncertainty in the model by optimising the worst-case risk over a posterior-informed ambiguity set. We show that our method admits a closed-form dual representation for many exponential family members and showcase its improved out-of-sample robustness against existing Bayesian DRO methodology in the Newsvendor problem.
An Expectation-Based Network Scan Statistic for a COVID-19 Early Warning System
Dec 08, 2020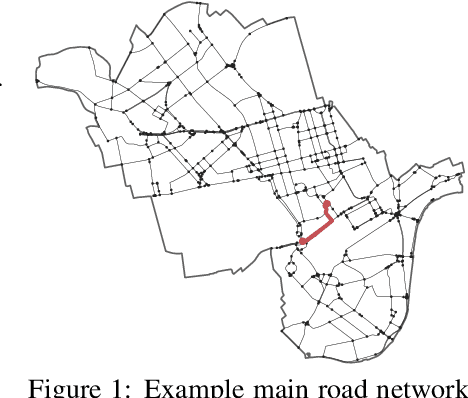
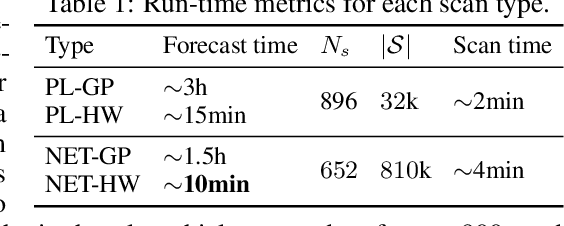
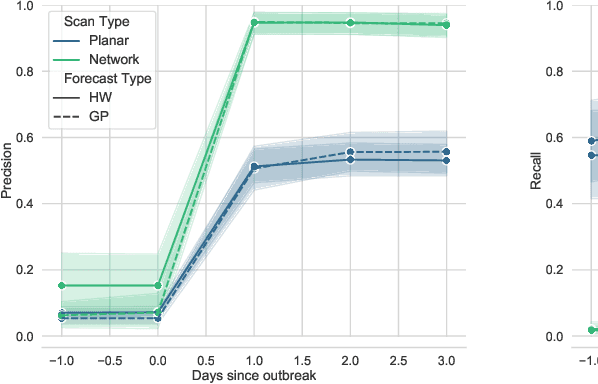
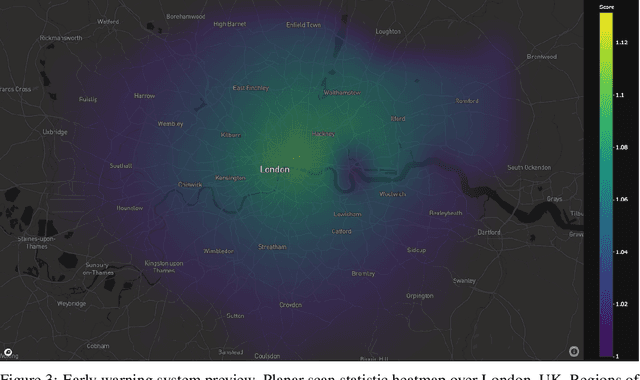
Abstract:One of the Greater London Authority's (GLA) response to the COVID-19 pandemic brings together multiple large-scale and heterogeneous datasets capturing mobility, transportation and traffic activity over the city of London to better understand 'busyness' and enable targeted interventions and effective policy-making. As part of Project Odysseus we describe an early-warning system and introduce an expectation-based scan statistic for networks to help the GLA and Transport for London, understand the extent to which populations are following government COVID-19 guidelines. We explicitly treat the case of geographically fixed time-series data located on a (road) network and primarily focus on monitoring the dynamics across large regions of the capital. Additionally, we also focus on the detection and reporting of significant spatio-temporal regions. Our approach is extending the Network Based Scan Statistic (NBSS) by making it expectation-based (EBP) and by using stochastic processes for time-series forecasting, which enables us to quantify metric uncertainty in both the EBP and NBSS frameworks. We introduce a variant of the metric used in the EBP model which focuses on identifying space-time regions in which activity is quieter than expected.
Near Real-Time Social Distancing in London
Dec 07, 2020
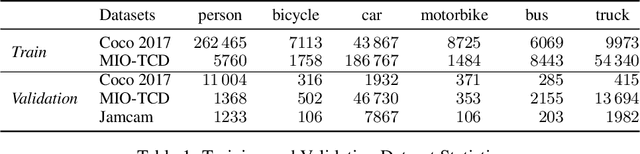
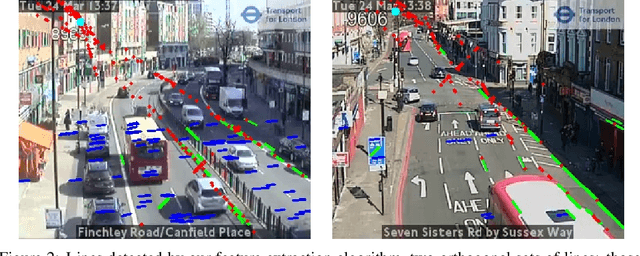
Abstract:During the COVID-19 pandemic, policy makers at the Greater London Authority, the regional governance body of London, UK, are reliant upon prompt and accurate data sources. Large well-defined heterogeneous compositions of activity throughout the city are sometimes difficult to acquire, yet are a necessity in order to learn 'busyness' and consequently make safe policy decisions. One component of our project within this space is to utilise existing infrastructure to estimate social distancing adherence by the general public. Our method enables near immediate sampling and contextualisation of activity and physical distancing on the streets of London via live traffic camera feeds. We introduce a framework for inspecting and improving upon existing methods, whilst also describing its active deployment on over 900 real-time feeds.
On the Constrained Least-cost Tour Problem
Jun 18, 2019
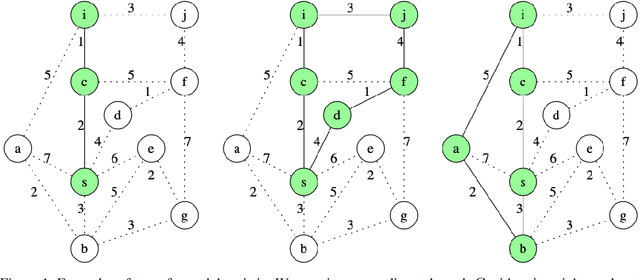
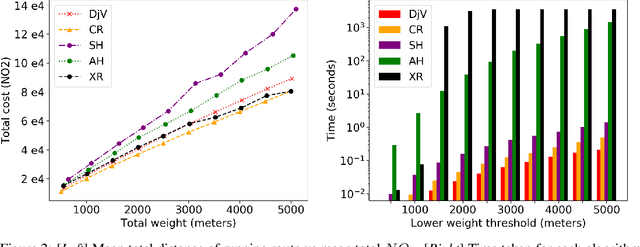
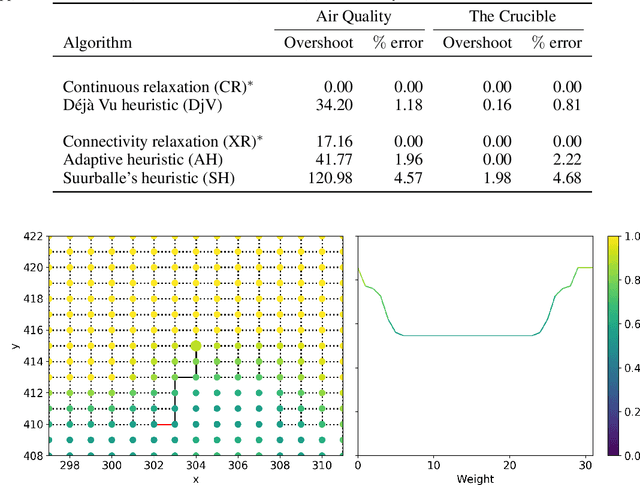
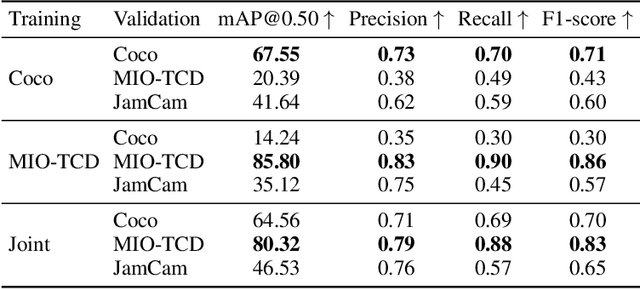
Abstract:We introduce the Constrained Least-cost Tour (CLT) problem: given an undirected graph with weight and cost functions on the edges, minimise the total cost of a tour rooted at a start vertex such that the total weight lies within a given range. CLT is related to the family of Travelling Salesman Problems with Profits, but differs by defining the weight function on edges instead of vertices, and by requiring the total weight to be within a range instead of being at least some quota. We prove CLT is $\mathcal{NP}$-hard, even in the simple case when the input graph is a path. We derive an informative lower bound by relaxing the integrality of edges and propose a heuristic motivated by this relaxation. For the case that requires the tour to be a simple cycle, we develop two heuristics which exploit Suurballe's algorithm to find low-cost, weight-feasible cycles. We demonstrate our algorithms by addressing a real-world problem that affects urban populations: finding routes that minimise air pollution exposure for walking, running and cycling in the city of London.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge