Spiking Neural Models for Decision-Making Tasks with Learning

In cognition, response times and choices in decision-making tasks are commonly modeled using Drift Diffusion Models (DDMs), which describe the accumulation of evidence for a decision as a stochastic process, specifically a Brownian motion, with the drift rate reflecting the strength of the evidence. In the same vein, the Poisson counter model describes the accumulation of evidence as discrete events whose counts over time are modeled as Poisson processes, and has a spiking neurons interpretation as these processes are used to model neuronal activities. However, these models lack a learning mechanism and are limited to tasks where participants have prior knowledge of the categories. To bridge the gap between cognitive and biological models, we propose a biologically plausible Spiking Neural Network (SNN) model for decision-making that incorporates a learning mechanism and whose neurons activities are modeled by a multivariate Hawkes process. First, we show a coupling result between the DDM and the Poisson counter model, establishing that these two models provide similar categorizations and reaction times and that the DDM can be approximated by spiking Poisson neurons. To go further, we show that a particular DDM with correlated noise can be derived from a Hawkes network of spiking neurons governed by a local learning rule. In addition, we designed an online categorization task to evaluate the model predictions. This work provides a significant step toward integrating biologically relevant neural mechanisms into cognitive models, fostering a deeper understanding of the relationship between neural activity and behavior.

Model selection for behavioral learning data and applications to contextual bandits

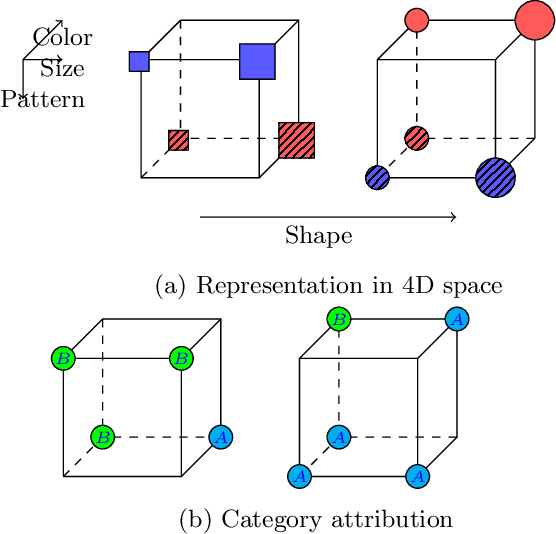
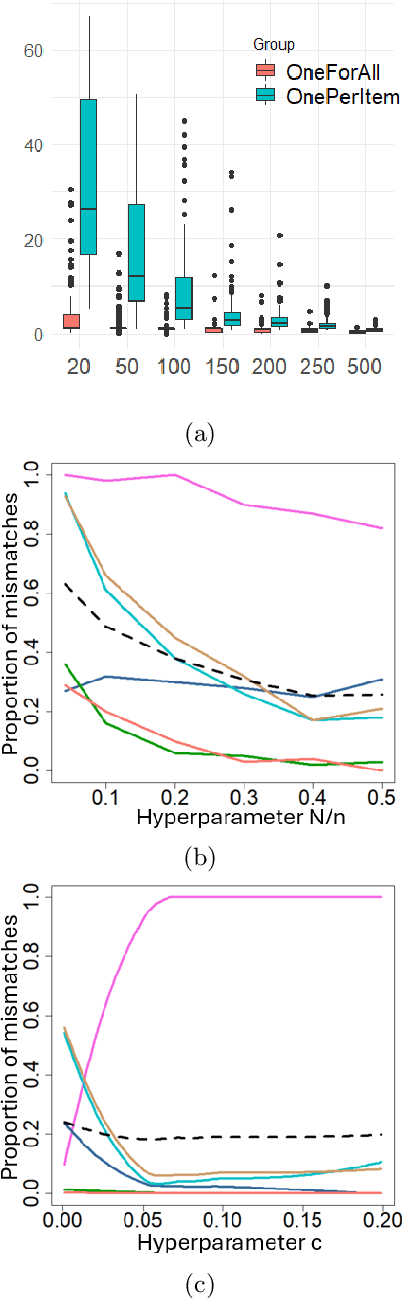
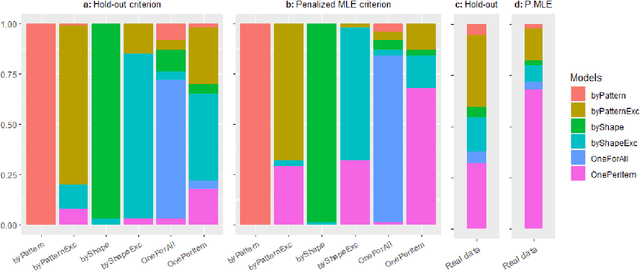
Learning for animals or humans is the process that leads to behaviors better adapted to the environment. This process highly depends on the individual that learns and is usually observed only through the individual's actions. This article presents ways to use this individual behavioral data to find the model that best explains how the individual learns. We propose two model selection methods: a general hold-out procedure and an AIC-type criterion, both adapted to non-stationary dependent data. We provide theoretical error bounds for these methods that are close to those of the standard i.i.d. case. To compare these approaches, we apply them to contextual bandit models and illustrate their use on both synthetic and experimental learning data in a human categorization task.

CHANI: Correlation-based Hawkes Aggregation of Neurons with bio-Inspiration

The present work aims at proving mathematically that a neural network inspired by biology can learn a classification task thanks to local transformations only. In this purpose, we propose a spiking neural network named CHANI (Correlation-based Hawkes Aggregation of Neurons with bio-Inspiration), whose neurons activity is modeled by Hawkes processes. Synaptic weights are updated thanks to an expert aggregation algorithm, providing a local and simple learning rule. We were able to prove that our network can learn on average and asymptotically. Moreover, we demonstrated that it automatically produces neuronal assemblies in the sense that the network can encode several classes and that a same neuron in the intermediate layers might be activated by more than one class, and we provided numerical simulations on synthetic dataset. This theoretical approach contrasts with the traditional empirical validation of biologically inspired networks and paves the way for understanding how local learning rules enable neurons to form assemblies able to represent complex concepts.

On the convergence of the MLE as an estimator of the learning rate in the Exp3 algorithm

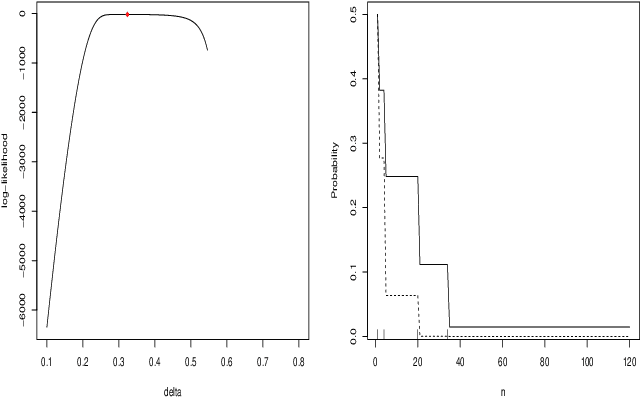
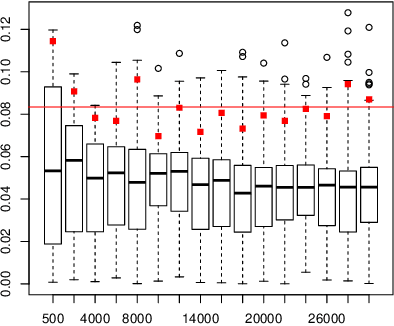
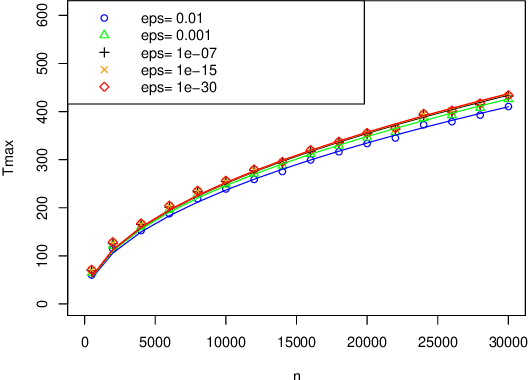
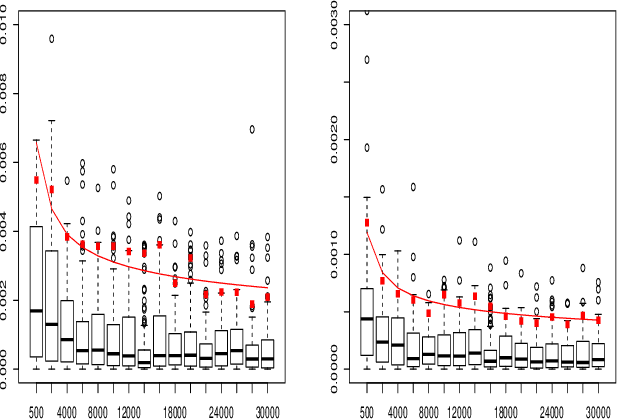
When fitting the learning data of an individual to algorithm-like learning models, the observations are so dependent and non-stationary that one may wonder what the classical Maximum Likelihood Estimator (MLE) could do, even if it is the usual tool applied to experimental cognition. Our objective in this work is to show that the estimation of the learning rate cannot be efficient if the learning rate is constant in the classical Exp3 (Exponential weights for Exploration and Exploitation) algorithm. Secondly, we show that if the learning rate decreases polynomially with the sample size, then the prediction error and in some cases the estimation error of the MLE satisfy bounds in probability that decrease at a polynomial rate.

Sliding window strategy for convolutional spike sorting with Lasso : Algorithm, theoretical guarantees and complexity

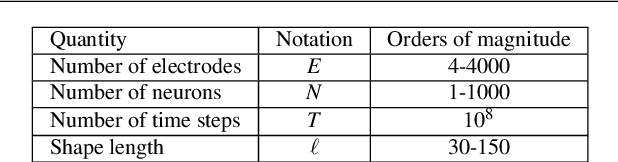
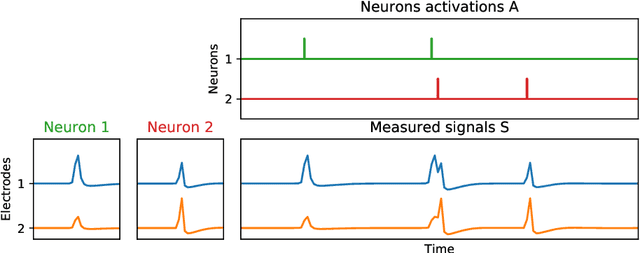
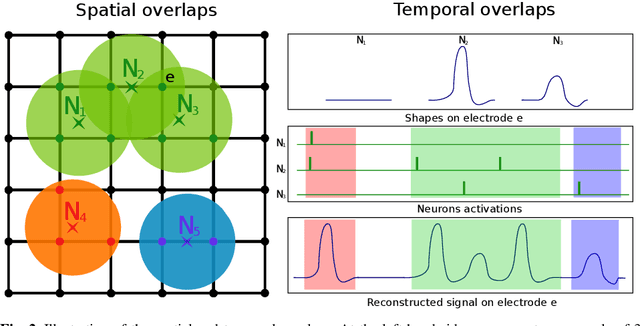
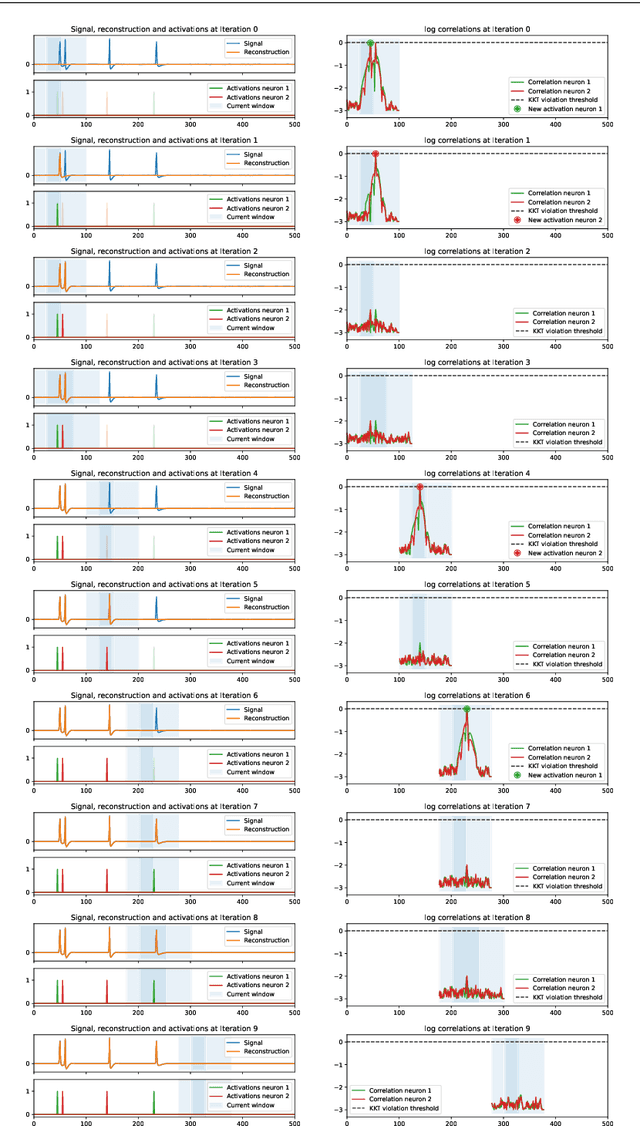
We present a fast algorithm for the resolution of the Lasso for convolutional models in high dimension, with a particular focus on the problem of spike sorting in neuroscience. Making use of biological properties related to neurons, we explain how the particular structure of the problem allows several optimizations, leading to an algorithm with a temporal complexity which grows linearly with respect to the size of the recorded signal and can be performed online. Moreover the spatial separability of the initial problem allows to break it into subproblems, further reducing the complexity and making possible its application on the latest recording devices which comprise a large number of sensors. We provide several mathematical results: the size and numerical complexity of the subproblems can be estimated mathematically by using percolation theory. We also show under reasonable assumptions that the Lasso estimator retrieves the true support with large probability. Finally the theoretical time complexity of the algorithm is given. Numerical simulations are also provided in order to illustrate the efficiency of our approach.

Event-scheduling algorithms with Kalikow decomposition for simulating potentially infinite neuronal networks

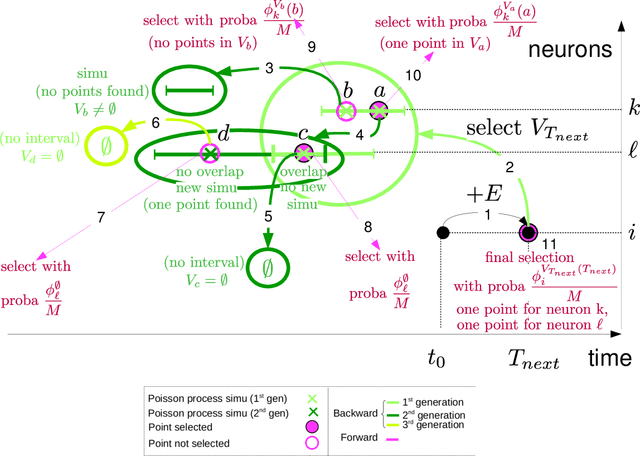
Event-scheduling algorithms can compute in continuous time the next occurrence of points (as events) of a counting process based on their current conditional intensity. In particular event-scheduling algorithms can be adapted to perform the simulation of finite neuronal networks activity. These algorithms are based on Ogata's thinning strategy \cite{Oga81}, which always needs to simulate the whole network to access the behaviour of one particular neuron of the network. On the other hand, for discrete time models, theoretical algorithms based on Kalikow decomposition can pick at random influencing neurons and perform a perfect simulation (meaning without approximations) of the behaviour of one given neuron embedded in an infinite network, at every time step. These algorithms are currently not computationally tractable in continuous time. To solve this problem, an event-scheduling algorithm with Kalikow decomposition is proposed here for the sequential simulation of point processes neuronal models satisfying this decomposition. This new algorithm is applied to infinite neuronal networks whose finite time simulation is a prerequisite to realistic brain modeling.

Large scale Lasso with windowed active set for convolutional spike sorting

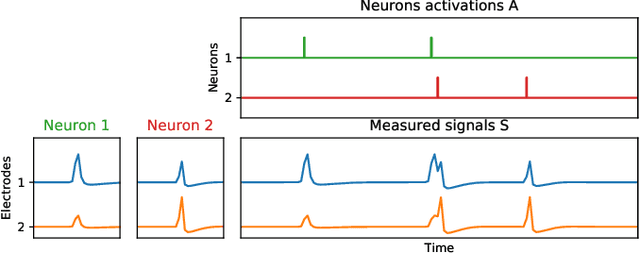
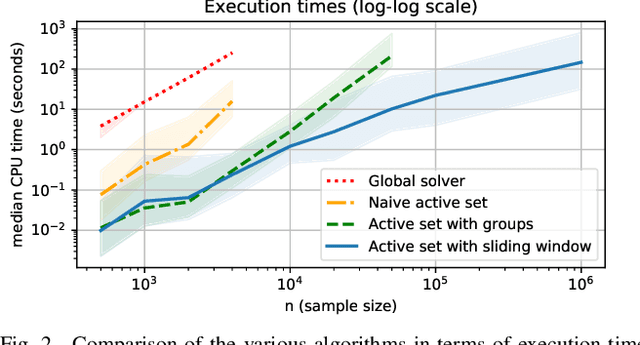
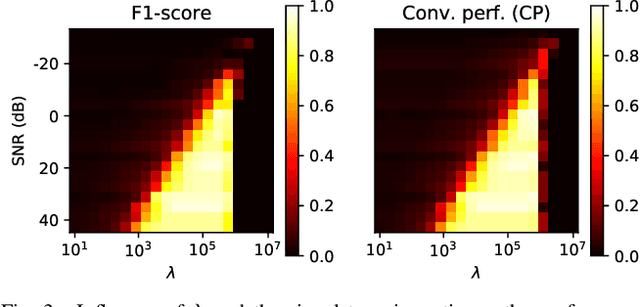
Spike sorting is a fundamental preprocessing step in neuroscience that is central to access simultaneous but distinct neuronal activities and therefore to better understand the animal or even human brain. But numerical complexity limits studies that require processing large scale datasets in terms of number of electrodes, neurons, spikes and length of the recorded signals. We propose in this work a novel active set algorithm aimed at solving the Lasso for a classical convolutional model. Our algorithm can be implemented efficiently on parallel architecture and has a linear complexity w.r.t. the temporal dimensionality which ensures scaling and will open the door to online spike sorting. We provide theoretical results about the complexity of the algorithm and illustrate it in numerical experiments along with results about the accuracy of the spike recovery and robustness to the regularization parameter.

Microscopic approach of a time elapsed neural model

The spike trains are the main components of the information processing in the brain. To model spike trains several point processes have been investigated in the literature. And more macroscopic approaches have also been studied, using partial differential equation models. The main aim of the present article is to build a bridge between several point processes models (Poisson, Wold, Hawkes) that have been proved to statistically fit real spike trains data and age-structured partial differential equations as introduced by Pakdaman, Perthame and Salort.