Model selection for behavioral learning data and applications to contextual bandits

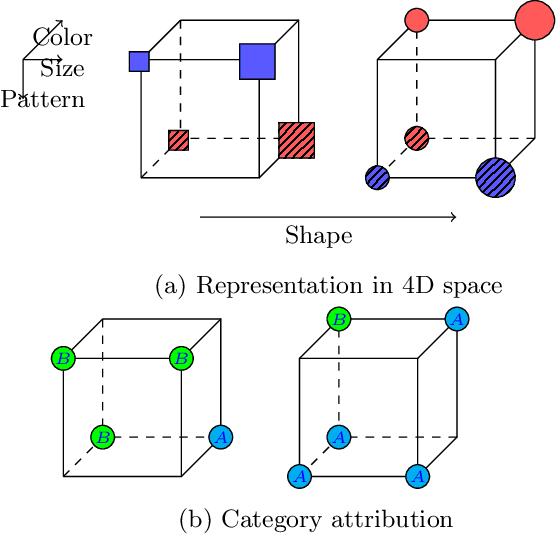
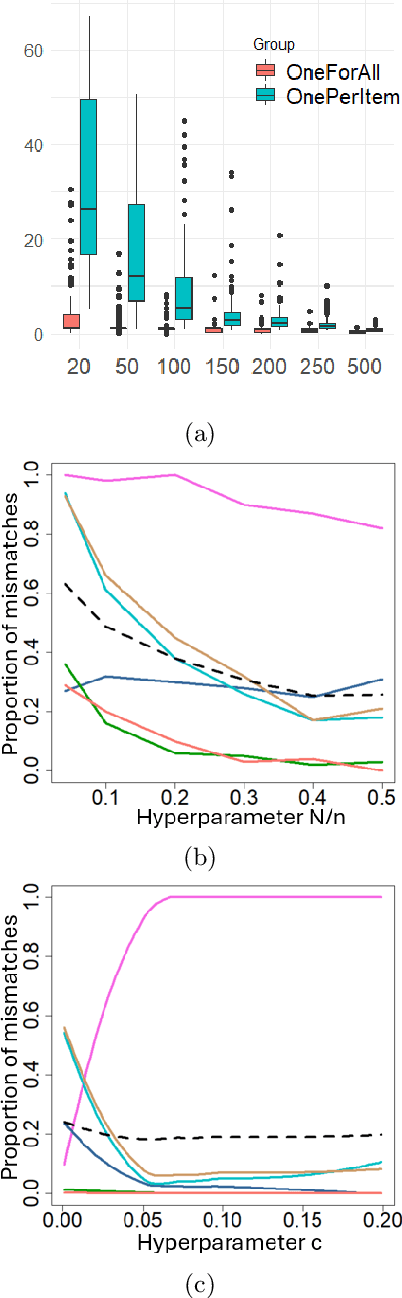
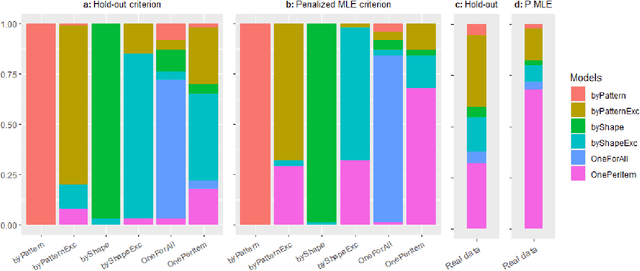
Learning for animals or humans is the process that leads to behaviors better adapted to the environment. This process highly depends on the individual that learns and is usually observed only through the individual's actions. This article presents ways to use this individual behavioral data to find the model that best explains how the individual learns. We propose two model selection methods: a general hold-out procedure and an AIC-type criterion, both adapted to non-stationary dependent data. We provide theoretical error bounds for these methods that are close to those of the standard i.i.d. case. To compare these approaches, we apply them to contextual bandit models and illustrate their use on both synthetic and experimental learning data in a human categorization task.

On the convergence of the MLE as an estimator of the learning rate in the Exp3 algorithm

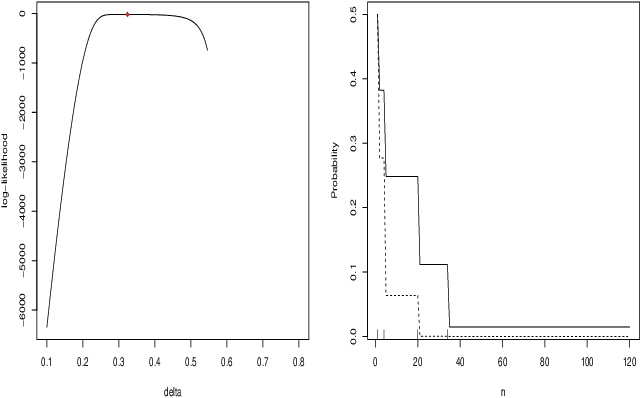
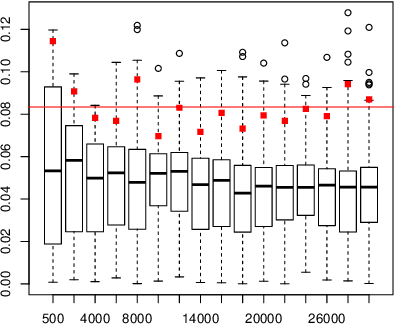
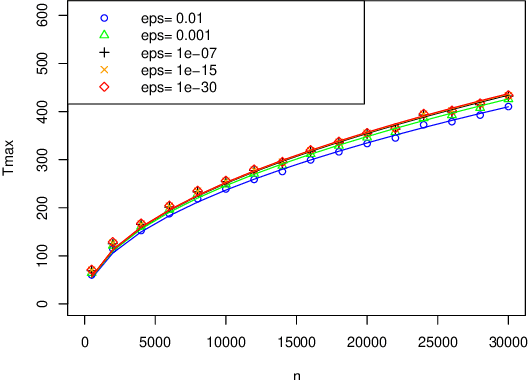
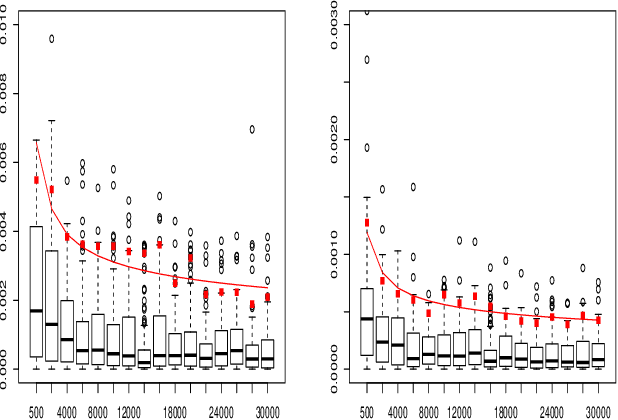
When fitting the learning data of an individual to algorithm-like learning models, the observations are so dependent and non-stationary that one may wonder what the classical Maximum Likelihood Estimator (MLE) could do, even if it is the usual tool applied to experimental cognition. Our objective in this work is to show that the estimation of the learning rate cannot be efficient if the learning rate is constant in the classical Exp3 (Exponential weights for Exploration and Exploitation) algorithm. Secondly, we show that if the learning rate decreases polynomially with the sample size, then the prediction error and in some cases the estimation error of the MLE satisfy bounds in probability that decrease at a polynomial rate.