Architecture independent generalization bounds for overparametrized deep ReLU networks

We prove that overparametrized neural networks are able to generalize with a test error that is independent of the level of overparametrization, and independent of the Vapnik-Chervonenkis (VC) dimension. We prove explicit bounds that only depend on the metric geometry of the test and training sets, on the regularity properties of the activation function, and on the operator norms of the weights and norms of biases. For overparametrized deep ReLU networks with a training sample size bounded by the input space dimension, we explicitly construct zero loss minimizers without use of gradient descent, and prove that the generalization error is independent of the network architecture.

Interpretable global minima of deep ReLU neural networks on sequentially separable data

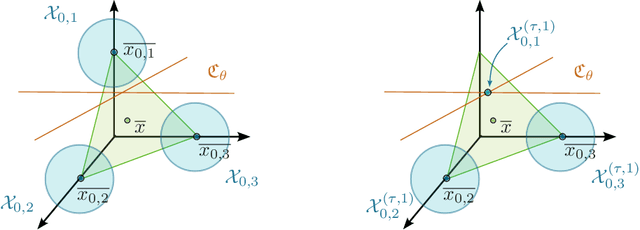
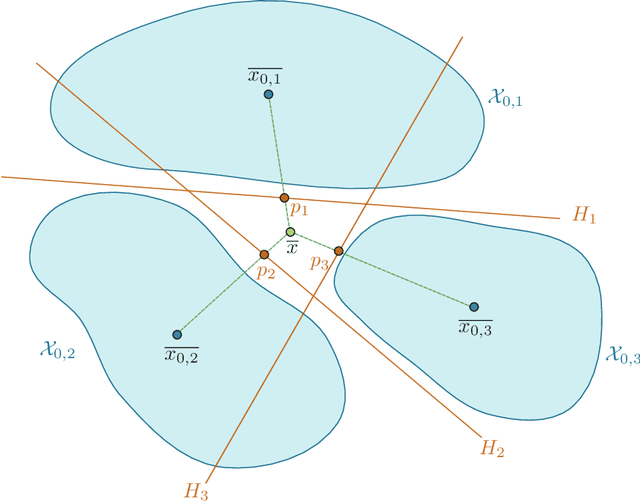
We explicitly construct zero loss neural network classifiers. We write the weight matrices and bias vectors in terms of cumulative parameters, which determine truncation maps acting recursively on input space. The configurations for the training data considered are (i) sufficiently small, well separated clusters corresponding to each class, and (ii) equivalence classes which are sequentially linearly separable. In the best case, for $Q$ classes of data in $\mathbb{R}^M$, global minimizers can be described with $Q(M+2)$ parameters.

Non-approximability of constructive global $\mathcal{L}^2$ minimizers by gradient descent in Deep Learning

We analyze geometric aspects of the gradient descent algorithm in Deep Learning (DL) networks. In particular, we prove that the globally minimizing weights and biases for the $\mathcal{L}^2$ cost obtained constructively in [Chen-Munoz Ewald 2023] for underparametrized ReLU DL networks can generically not be approximated via the gradient descent flow. We therefore conclude that the method introduced in [Chen-Munoz Ewald 2023] is disjoint from the gradient descent method.

Geometric structure of Deep Learning networks and construction of global ${\mathcal L}^2$ minimizers

In this paper, we provide a geometric interpretation of the structure of Deep Learning (DL) networks, characterized by $L$ hidden layers, a ramp activation function, an ${\mathcal L}^2$ Schatten class (or Hilbert-Schmidt) cost function, and input and output spaces ${\mathbb R}^Q$ with equal dimension $Q\geq1$. The hidden layers are defined on spaces ${\mathbb R}^{Q}$, as well. We apply our recent results on shallow neural networks to construct an explicit family of minimizers for the global minimum of the cost function in the case $L\geq Q$, which we show to be degenerate. In the context presented here, the hidden layers of the DL network "curate" the training inputs by recursive application of a truncation map that minimizes the noise to signal ratio of the training inputs. Moreover, we determine a set of $2^Q-1$ distinct degenerate local minima of the cost function.

Geometric structure of shallow neural networks and constructive ${\mathcal L}^2$ cost minimization

In this paper, we provide a geometric interpretation of the structure of shallow neural networks characterized by one hidden layer, a ramp activation function, an ${\mathcal L}^2$ Schatten class (or Hilbert-Schmidt) cost function, input space ${\mathbb R}^M$, output space ${\mathbb R}^Q$ with $Q\leq M$, and training input sample size $N>QM$. We prove an upper bound on the minimum of the cost function of order $O(\delta_P$ where $\delta_P$ measures the signal to noise ratio of training inputs. We obtain an approximate optimizer using projections adapted to the averages $\overline{x_{0,j}}$ of training input vectors belonging to the same output vector $y_j$, $j=1,\dots,Q$. In the special case $M=Q$, we explicitly determine an exact degenerate local minimum of the cost function; the sharp value differs from the upper bound obtained for $Q\leq M$ by a relative error $O(\delta_P^2)$. The proof of the upper bound yields a constructively trained network; we show that it metrizes the $Q$-dimensional subspace in the input space ${\mathbb R}^M$ spanned by $\overline{x_{0,j}}$, $j=1,\dots,Q$. We comment on the characterization of the global minimum of the cost function in the given context.