Bayesian inference of ODEs with Gaussian processes

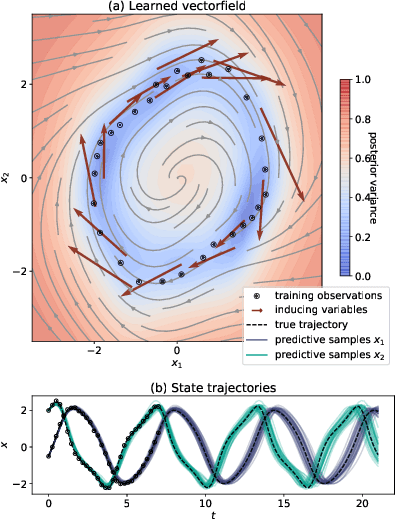
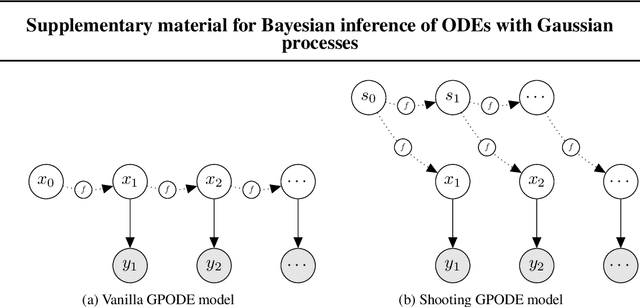
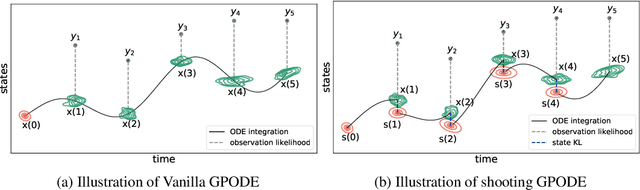
Recent machine learning advances have proposed black-box estimation of unknown continuous-time system dynamics directly from data. However, earlier works are based on approximative ODE solutions or point estimates. We propose a novel Bayesian nonparametric model that uses Gaussian processes to infer posteriors of unknown ODE systems directly from data. We derive sparse variational inference with decoupled functional sampling to represent vector field posteriors. We also introduce a probabilistic shooting augmentation to enable efficient inference from arbitrarily long trajectories. The method demonstrates the benefit of computing vector field posteriors, with predictive uncertainty scores outperforming alternative methods on multiple ODE learning tasks.

Deep learning with differential Gaussian process flows

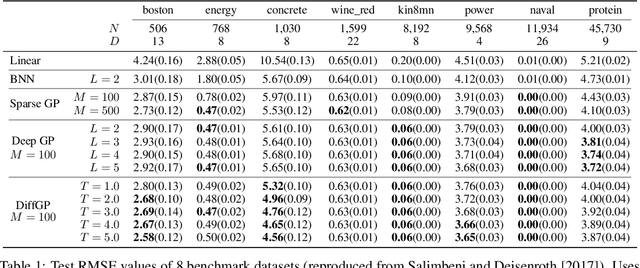
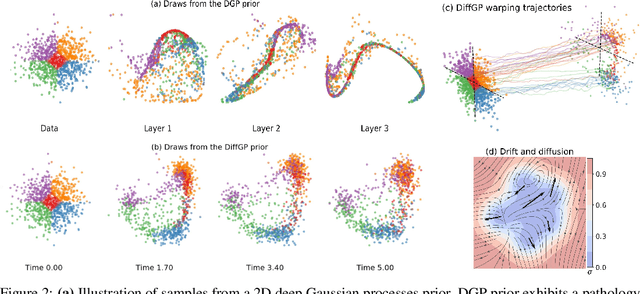
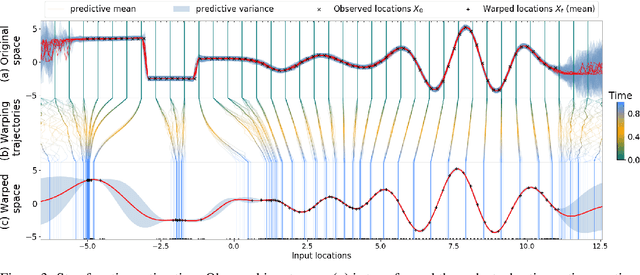
We propose a novel deep learning paradigm of differential flows that learn a stochastic differential equation transformations of inputs prior to a standard classification or regression function. The key property of differential Gaussian processes is the warping of inputs through infinitely deep, but infinitesimal, differential fields, that generalise discrete layers into a dynamical system. We demonstrate state-of-the-art results that exceed the performance of deep Gaussian processes and neural networks

Variational zero-inflated Gaussian processes with sparse kernels

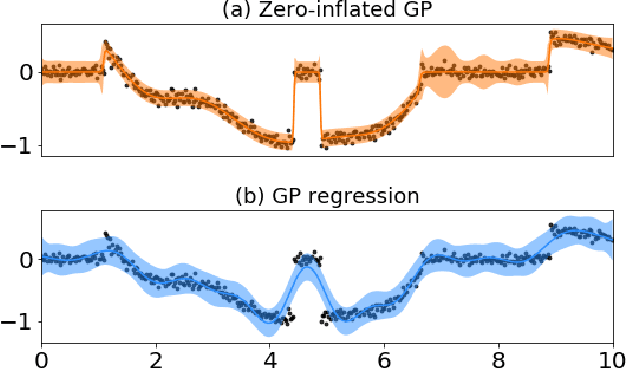
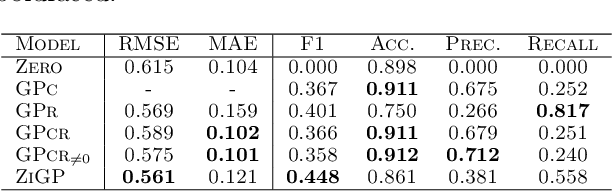
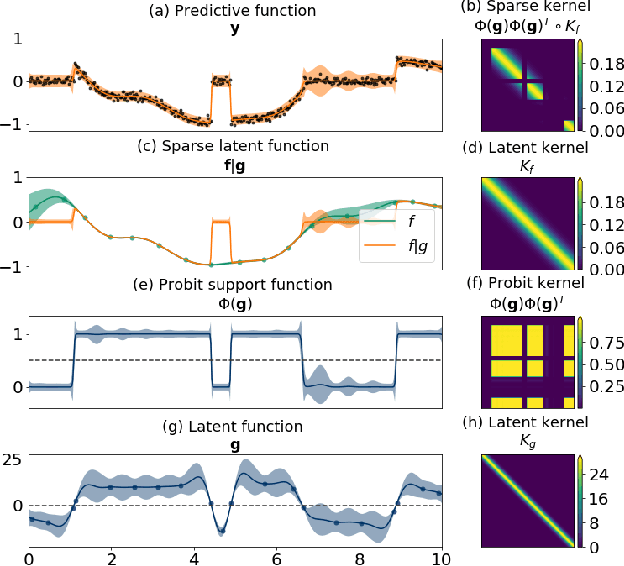
Zero-inflated datasets, which have an excess of zero outputs, are commonly encountered in problems such as climate or rare event modelling. Conventional machine learning approaches tend to overestimate the non-zeros leading to poor performance. We propose a novel model family of zero-inflated Gaussian processes (ZiGP) for such zero-inflated datasets, produced by sparse kernels through learning a latent probit Gaussian process that can zero out kernel rows and columns whenever the signal is absent. The ZiGPs are particularly useful for making the powerful Gaussian process networks more interpretable. We introduce sparse GP networks where variable-order latent modelling is achieved through sparse mixing signals. We derive the non-trivial stochastic variational inference tractably for scalable learning of the sparse kernels in both models. The novel output-sparse approach improves both prediction of zero-inflated data and interpretability of latent mixing models.