Weighted Random Dot Product Graphs

Modeling of intricate relational patterns has become a cornerstone of contemporary statistical research and related data science fields. Networks, represented as graphs, offer a natural framework for this analysis. This paper extends the Random Dot Product Graph (RDPG) model to accommodate weighted graphs, markedly broadening the model's scope to scenarios where edges exhibit heterogeneous weight distributions. We propose a nonparametric weighted (W)RDPG model that assigns a sequence of latent positions to each node. Inner products of these nodal vectors specify the moments of their incident edge weights' distribution via moment-generating functions. In this way, and unlike prior art, the WRDPG can discriminate between weight distributions that share the same mean but differ in other higher-order moments. We derive statistical guarantees for an estimator of the nodal's latent positions adapted from the workhorse adjacency spectral embedding, establishing its consistency and asymptotic normality. We also contribute a generative framework that enables sampling of graphs that adhere to a (prescribed or data-fitted) WRDPG, facilitating, e.g., the analysis and testing of observed graph metrics using judicious reference distributions. The paper is organized to formalize the model's definition, the estimation (or nodal embedding) process and its guarantees, as well as the methodologies for generating weighted graphs, all complemented by illustrative and reproducible examples showcasing the WRDPG's effectiveness in various network analytic applications.

Probabilistic Insights for Efficient Exploration Strategies in Reinforcement Learning

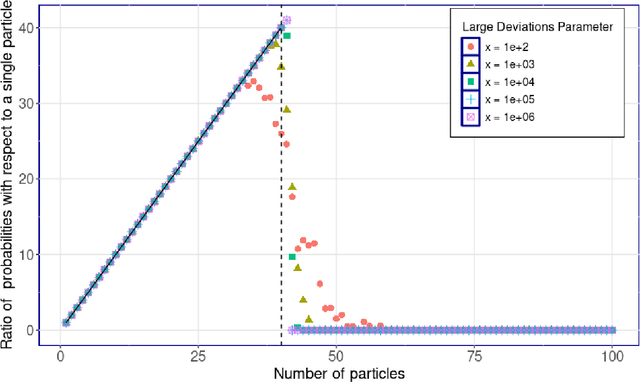
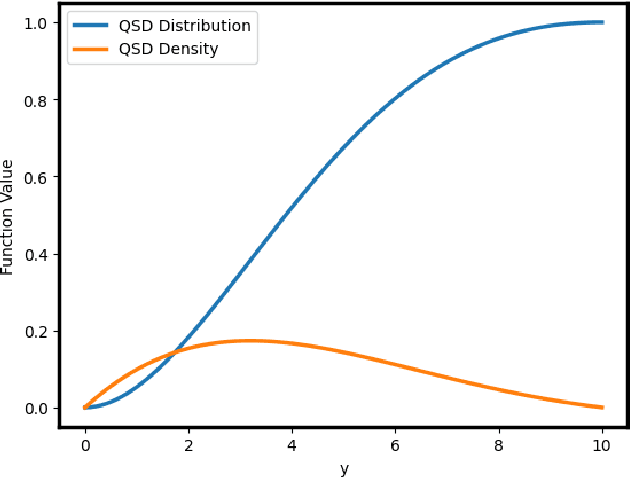
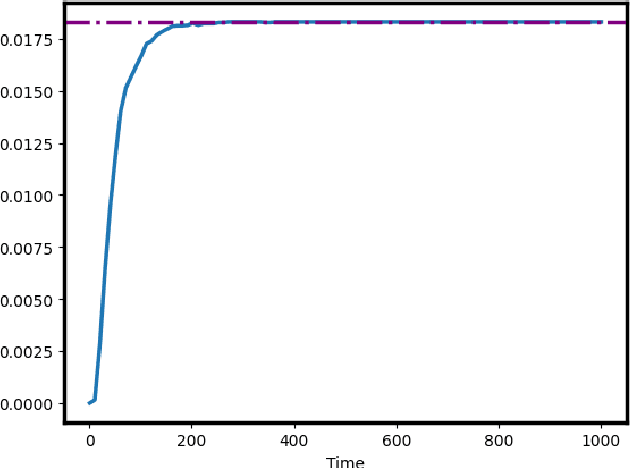
We investigate efficient exploration strategies of environments with unknown stochastic dynamics and sparse rewards. Specifically, we analyze first the impact of parallel simulations on the probability of reaching rare states within a finite time budget. Using simplified models based on random walks and L\'evy processes, we provide analytical results that demonstrate a phase transition in reaching probabilities as a function of the number of parallel simulations. We identify an optimal number of parallel simulations that balances exploration diversity and time allocation. Additionally, we analyze a restarting mechanism that exponentially enhances the probability of success by redirecting efforts toward more promising regions of the state space. Our findings contribute to a more qualitative and quantitative theory of some exploration schemes in reinforcement learning, offering insights into developing more efficient strategies for environments characterized by rare events.

Gradient-Based Spectral Embeddings of Random Dot Product Graphs

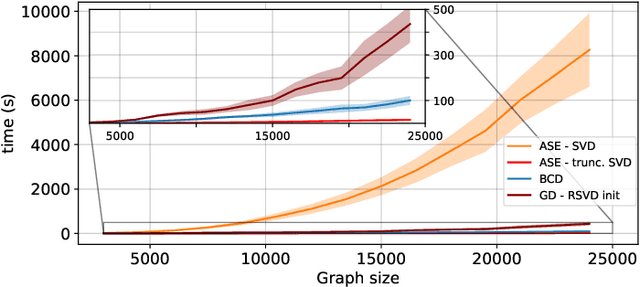
The Random Dot Product Graph (RDPG) is a generative model for relational data, where nodes are represented via latent vectors in low-dimensional Euclidean space. RDPGs crucially postulate that edge formation probabilities are given by the dot product of the corresponding latent positions. Accordingly, the embedding task of estimating these vectors from an observed graph is typically posed as a low-rank matrix factorization problem. The workhorse Adjacency Spectral Embedding (ASE) enjoys solid statistical properties, but it is formally solving a surrogate problem and can be computationally intensive. In this paper, we bring to bear recent advances in non-convex optimization and demonstrate their impact to RDPG inference. We advocate first-order gradient descent methods to better solve the embedding problem, and to organically accommodate broader network embedding applications of practical relevance. Notably, we argue that RDPG embeddings of directed graphs loose interpretability unless the factor matrices are constrained to have orthogonal columns. We thus develop a novel feasible optimization method in the resulting manifold. The effectiveness of the graph representation learning framework is demonstrated on reproducible experiments with both synthetic and real network data. Our open-source algorithm implementations are scalable, and unlike the ASE they are robust to missing edge data and can track slowly-varying latent positions from streaming graphs.

Online Change Point Detection for Weighted and Directed Random Dot Product Graphs

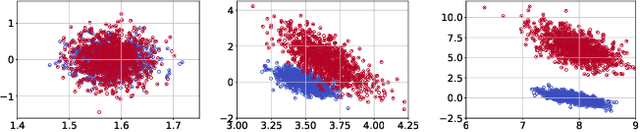
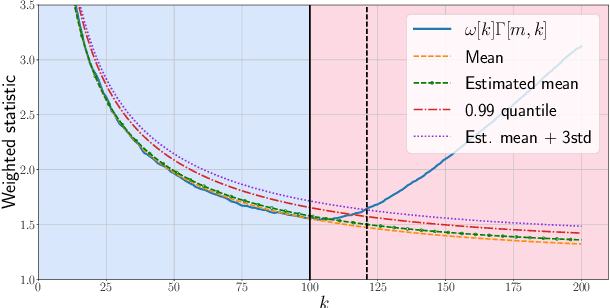
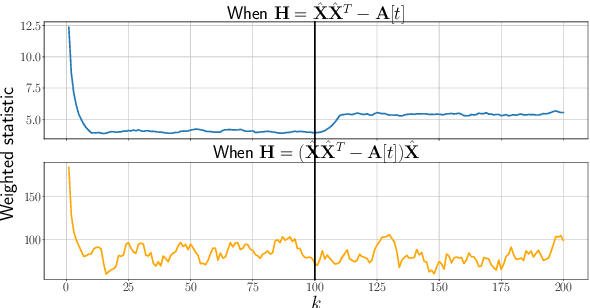
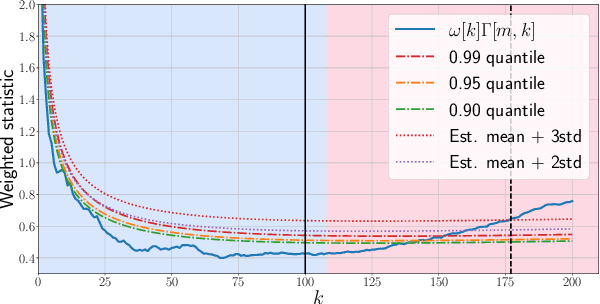
Given a sequence of random (directed and weighted) graphs, we address the problem of online monitoring and detection of changes in the underlying data distribution. Our idea is to endow sequential change-point detection (CPD) techniques with a graph representation learning substrate based on the versatile Random Dot Product Graph (RDPG) model. We consider efficient, online updates of a judicious monitoring function, which quantifies the discrepancy between the streaming graph observations and the nominal RDPG. This reference distribution is inferred via spectral embeddings of the first few graphs in the sequence. We characterize the distribution of this running statistic to select thresholds that guarantee error-rate control, and under simplifying approximations we offer insights on the algorithm's detection resolution and delay. The end result is a lightweight online CPD algorithm, that is also explainable by virtue of the well-appreciated interpretability of RDPG embeddings. This is in stark contrast with most existing graph CPD approaches, which either rely on extensive computation, or they store and process the entire observed time series. An apparent limitation of the RDPG model is its suitability for undirected and unweighted graphs only, a gap we aim to close here to broaden the scope of the CPD framework. Unlike previous proposals, our non-parametric RDPG model for weighted graphs does not require a priori specification of the weights' distribution to perform inference and estimation. This network modeling contribution is of independent interest beyond CPD. We offer an open-source implementation of the novel online CPD algorithm for weighted and direct graphs, whose effectiveness and efficiency are demonstrated via (reproducible) synthetic and real network data experiments.