Pamuditha Somarathne
MOSAIC: Masked Optimisation with Selective Attention for Image Reconstruction
Jun 01, 2023



Abstract:Compressive sensing (CS) reconstructs images from sub-Nyquist measurements by solving a sparsity-regularized inverse problem. Traditional CS solvers use iterative optimizers with hand crafted sparsifiers, while early data-driven methods directly learn an inverse mapping from the low-dimensional measurement space to the original image space. The latter outperforms the former, but is restrictive to a pre-defined measurement domain. More recent, deep unrolling methods combine traditional proximal gradient methods and data-driven approaches to iteratively refine an image approximation. To achieve higher accuracy, it has also been suggested to learn both the sampling matrix, and the choice of measurement vectors adaptively. Contrary to the current trend, in this work we hypothesize that a general inverse mapping from a random set of compressed measurements to the image domain exists for a given measurement basis, and can be learned. Such a model is single-shot, non-restrictive and does not parametrize the sampling process. To this end, we propose MOSAIC, a novel compressive sensing framework to reconstruct images given any random selection of measurements, sampled using a fixed basis. Motivated by the uneven distribution of information across measurements, MOSAIC incorporates an embedding technique to efficiently apply attention mechanisms on an encoded sequence of measurements, while dispensing the need to use unrolled deep networks. A range of experiments validate our proposed architecture as a promising alternative for existing CS reconstruction methods, by achieving the state-of-the-art for metrics of reconstruction accuracy on standard datasets.
HPGNN: Using Hierarchical Graph Neural Networks for Outdoor Point Cloud Processing
Jun 05, 2022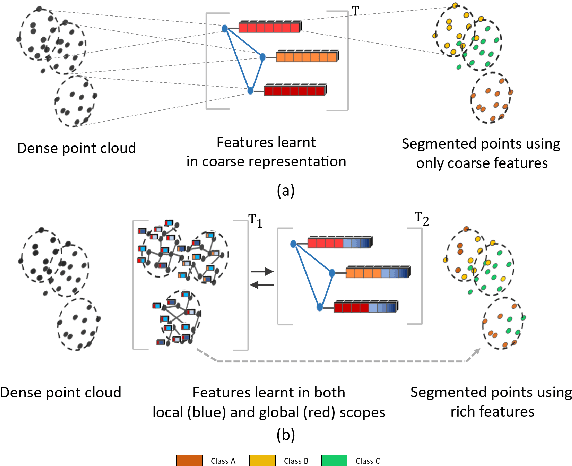

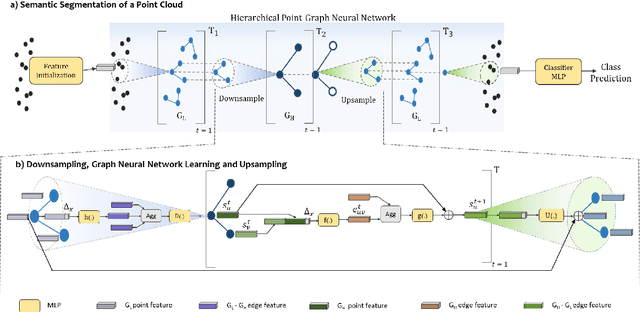
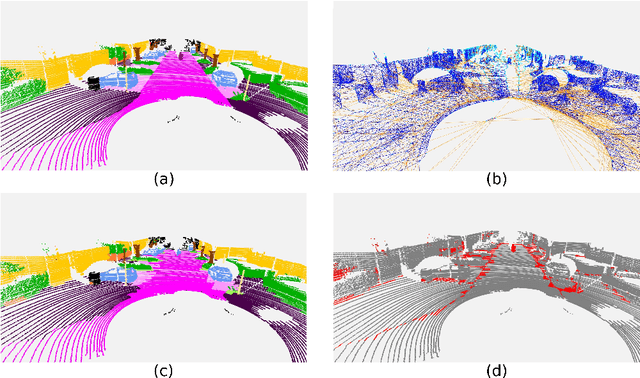
Abstract:Inspired by recent improvements in point cloud processing for autonomous navigation, we focus on using hierarchical graph neural networks for processing and feature learning over large-scale outdoor LiDAR point clouds. We observe that existing GNN based methods fail to overcome challenges of scale and irregularity of points in outdoor datasets. Addressing the need to preserve structural details while learning over a larger volume efficiently, we propose Hierarchical Point Graph Neural Network (HPGNN). It learns node features at various levels of graph coarseness to extract information. This enables to learn over a large point cloud while retaining fine details that existing point-level graph networks struggle to achieve. Connections between multiple levels enable a point to learn features in multiple scales, in a few iterations. We design HPGNN as a purely GNN-based approach, so that it offers modular expandability as seen with other point-based and Graph network baselines. To illustrate the improved processing capability, we compare previous point based and GNN models for semantic segmentation with our HPGNN, achieving a significant improvement for GNNs (+36.7 mIoU) on the SemanticKITTI dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge