Augmenting Neural Nets with Symbolic Synthesis: Applications to Few-Shot Learning

We propose symbolic learning as extensions to standard inductive learning models such as neural nets as a means to solve few shot learning problems. We device a class of visual discrimination puzzles that calls for recognizing objects and object relationships as well learning higher-level concepts from very few images. We propose a two-phase learning framework that combines models learned from large data sets using neural nets and symbolic first-order logic formulas learned from a few shot learning instance. We develop first-order logic synthesis techniques for discriminating images by using symbolic search and logic constraint solvers. By augmenting neural nets with them, we develop and evaluate a tool that can solve few shot visual discrimination puzzles with interpretable concepts.

Invariant Synthesis for Incomplete Verification Engines

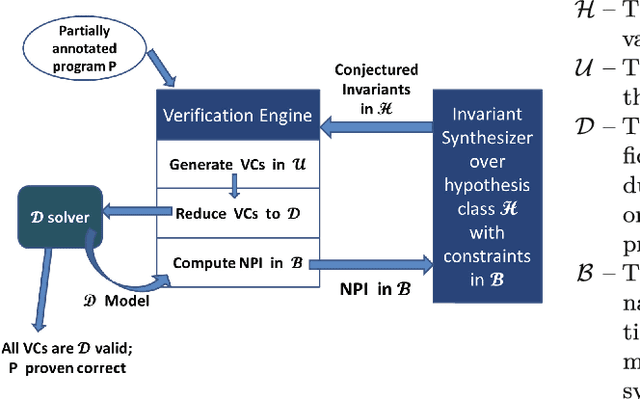
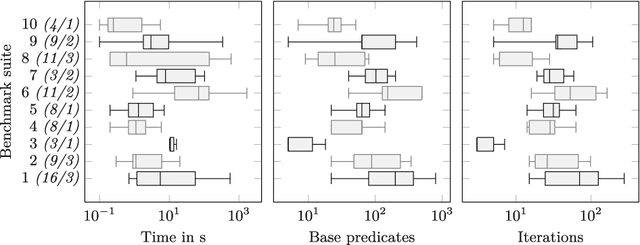
We propose a framework for synthesizing inductive invariants for incomplete verification engines, which soundly reduce logical problems in undecidable theories to decidable theories. Our framework is based on the counter-example guided inductive synthesis principle (CEGIS) and allows verification engines to communicate non-provability information to guide invariant synthesis. We show precisely how the verification engine can compute such non-provability information and how to build effective learning algorithms when invariants are expressed as Boolean combinations of a fixed set of predicates. Moreover, we evaluate our framework in two verification settings, one in which verification engines need to handle quantified formulas and one in which verification engines have to reason about heap properties expressed in an expressive but undecidable separation logic. Our experiments show that our invariant synthesis framework based on non-provability information can both effectively synthesize inductive invariants and adequately strengthen contracts across a large suite of programs.

Horn-ICE Learning for Synthesizing Invariants and Contracts

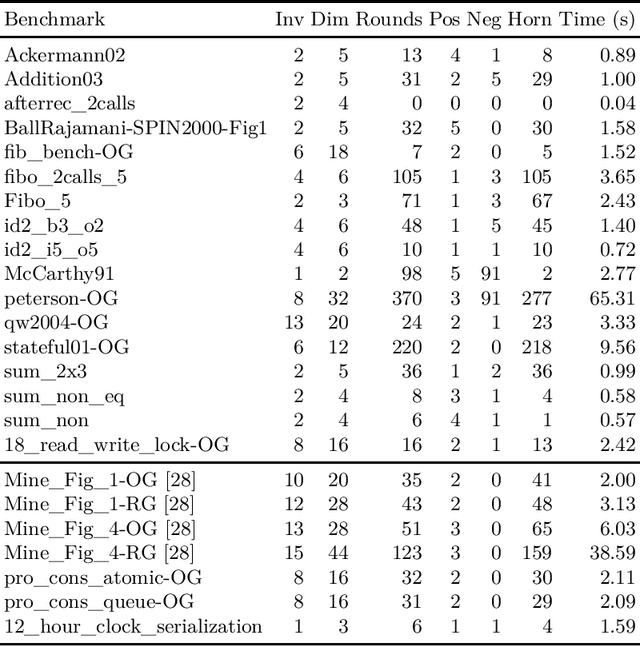
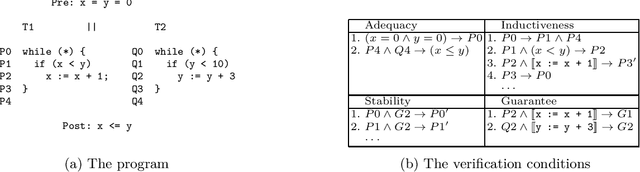
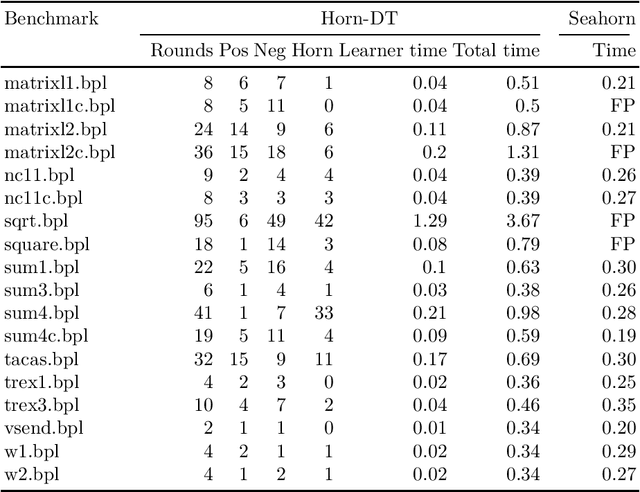
We design learning algorithms for synthesizing invariants using Horn implication counterexamples (Horn-ICE), extending the ICE-learning model. In particular, we describe a decision-tree learning algorithm that learns from Horn-ICE samples, works in polynomial time, and uses statistical heuristics to learn small trees that satisfy the samples. Since most verification proofs can be modeled using Horn clauses, Horn-ICE learning is a more robust technique to learn inductive annotations that prove programs correct. Our experiments show that an implementation of our algorithm is able to learn adequate inductive invariants and contracts efficiently for a variety of sequential and concurrent programs.

Learning Universally Quantified Invariants of Linear Data Structures

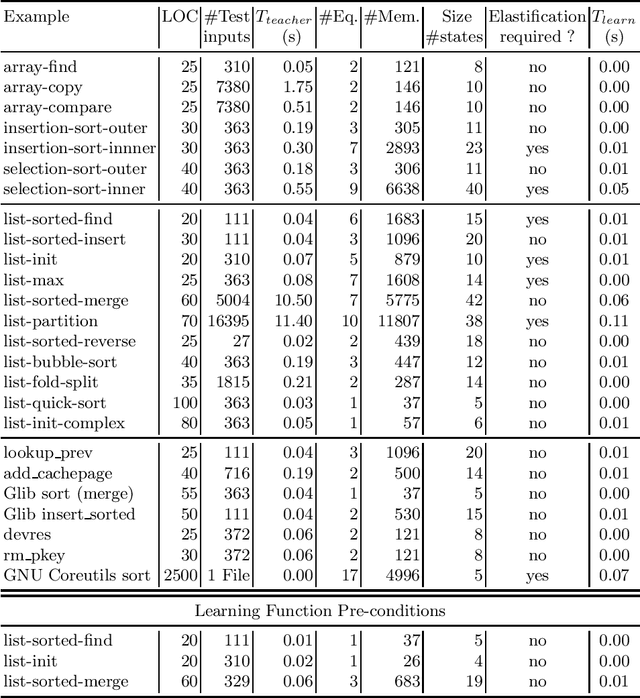
We propose a new automaton model, called quantified data automata over words, that can model quantified invariants over linear data structures, and build poly-time active learning algorithms for them, where the learner is allowed to query the teacher with membership and equivalence queries. In order to express invariants in decidable logics, we invent a decidable subclass of QDAs, called elastic QDAs, and prove that every QDA has a unique minimally-over-approximating elastic QDA. We then give an application of these theoretically sound and efficient active learning algorithms in a passive learning framework and show that we can efficiently learn quantified linear data structure invariants from samples obtained from dynamic runs for a large class of programs.