Inverting Cryptographic Hash Functions via Cube-and-Conquer

MD4 and MD5 are seminal cryptographic hash functions proposed in early 1990s. MD4 consists of 48 steps and produces a 128-bit hash given a message of arbitrary finite size. MD5 is a more secure 64-step extension of MD4. Both MD4 and MD5 are vulnerable to practical collision attacks, yet it is still not realistic to invert them, i.e. to find a message given a hash. In 2007, the 39-step version of MD4 was inverted via reducing to SAT and applying a CDCL solver along with the so-called Dobbertin's constraints. As for MD5, in 2012 its 28-step version was inverted via a CDCL solver for one specified hash without adding any additional constraints. In this study, Cube-and-Conquer (a combination of CDCL and lookahead) is applied to invert step-reduced versions of MD4 and MD5. For this purpose, two algorithms are proposed. The first one generates inversion problems for MD4 by gradually modifying the Dobbertin's constraints. The second algorithm tries the cubing phase of Cube-and-Conquer with different cutoff thresholds to find the one with minimal runtime estimation of the conquer phase. This algorithm operates in two modes: (i) estimating the hardness of an arbitrary given formula; (ii) incomplete SAT-solving of a given satisfiable formula. While the first algorithm is focused on inverting step-reduced MD4, the second one is not area-specific and so is applicable to a variety of classes of hard SAT instances. In this study, for the first time in history, 40-, 41-, 42-, and 43-step MD4 are inverted via the first algorithm and the estimating mode of the second algorithm. 28-step MD5 is inverted for four hashes via the incomplete SAT-solving mode of the second algorithm. For three hashes out of them this is done for the first time.

Translation of Algorithmic Descriptions of Discrete Functions to SAT with Applications to Cryptanalysis Problems

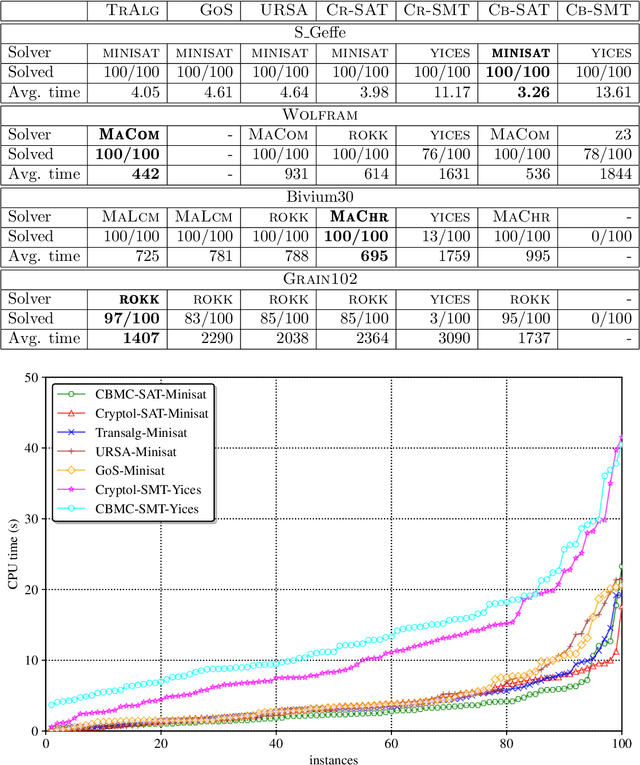
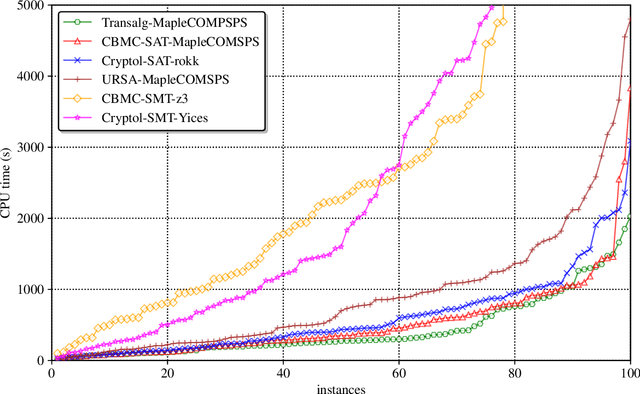
In the present paper we describe the technology for translating algorithmic descriptions of discrete functions to SAT. The proposed methods and algorithms of translation are aimed at application to the problems of SAT-based cryptanalysis. In the theoretical part of the paper we justify the main principles of general reduction to SAT for discrete functions from a class containing the majority of functions employed in cryptography. Based on these principles we describe the Transalg software system, developed with SAT-based cryptanalysis specifics in mind. We show the results of applications of Transalg to construction of a number of attacks on various cryptographic functions. Some of the corresponding attacks are state of the art. In the paper we also present the vast experimental data, obtained using the SAT-solvers that took first places at the SAT-competitions in the recent several years.

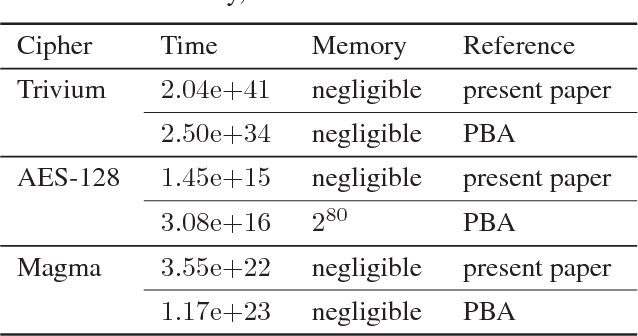
On Cryptographic Attacks Using Backdoors for SAT

Propositional satisfiability (SAT) is at the nucleus of state-of-the-art approaches to a variety of computationally hard problems, one of which is cryptanalysis. Moreover, a number of practical applications of SAT can only be tackled efficiently by identifying and exploiting a subset of formula's variables called backdoor set (or simply backdoors). This paper proposes a new class of backdoor sets for SAT used in the context of cryptographic attacks, namely guess-and-determine attacks. The idea is to identify the best set of backdoor variables subject to a statistically estimated hardness of the guess-and-determine attack using a SAT solver. Experimental results on weakened variants of the renowned encryption algorithms exhibit advantage of the proposed approach compared to the state of the art in terms of the estimated hardness of the resulting guess-and-determine attacks.

Encoding Cryptographic Functions to SAT Using Transalg System

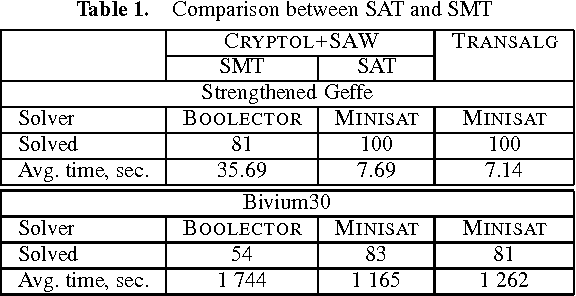
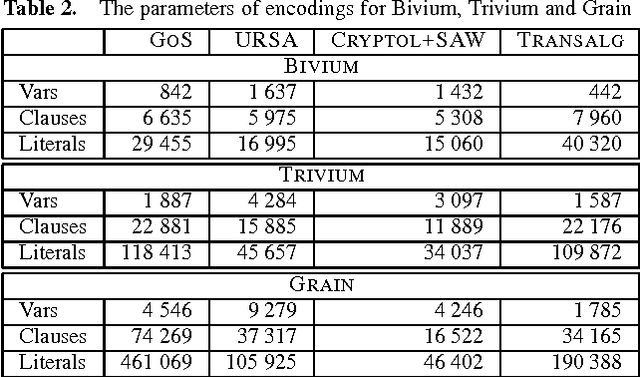
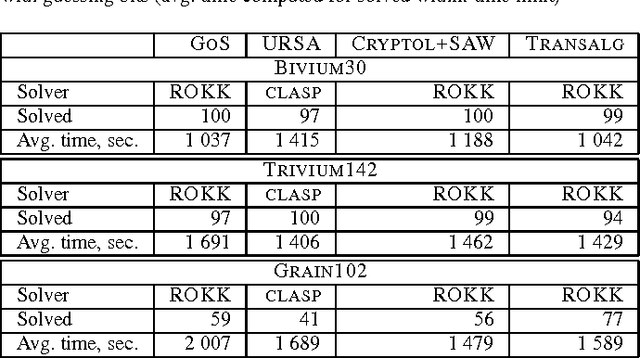
In this paper we propose the technology for constructing propositional encodings of discrete functions. It is aimed at solving inversion problems of considered functions using state-of-the-art SAT solvers. We implemented this technology in the form of the software system called Transalg, and used it to construct SAT encodings for a number of cryptanalysis problems. By applying SAT solvers to these encodings we managed to invert several cryptographic functions. In particular, we used the SAT encodings produced by Transalg to construct the family of two-block MD5 collisions in which the first 10 bytes are zeros. Also we used Transalg encoding for the widely known A5/1 keystream generator to solve several dozen of its cryptanalysis instances in a distributed computing environment. In the paper we compare in detail the functionality of Transalg with that of similar software systems.

Using Monte Carlo method for searching partitionings of hard variants of Boolean satisfiability problem

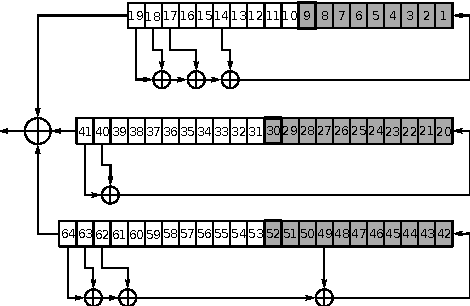
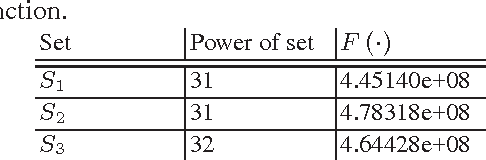
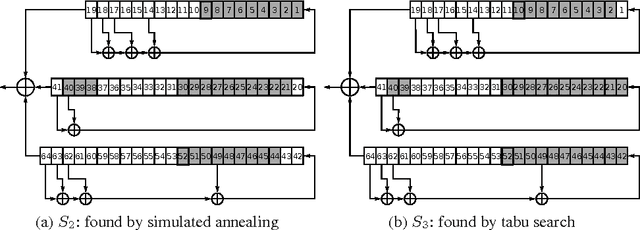
In this paper we propose the approach for constructing partitionings of hard variants of the Boolean satisfiability problem (SAT). Such partitionings can be used for solving corresponding SAT instances in parallel. For the same SAT instance one can construct different partitionings, each of them is a set of simplified versions of the original SAT instance. The effectiveness of an arbitrary partitioning is determined by the total time of solving of all SAT instances from it. We suggest the approach, based on the Monte Carlo method, for estimating time of processing of an arbitrary partitioning. With each partitioning we associate a point in the special finite search space. The estimation of effectiveness of the particular partitioning is the value of predictive function in the corresponding point of this space. The problem of search for an effective partitioning can be formulated as a problem of optimization of the predictive function. We use metaheuristic algorithms (simulated annealing and tabu search) to move from point to point in the search space. In our computational experiments we found partitionings for SAT instances encoding problems of inversion of some cryptographic functions. Several of these SAT instances with realistic predicted solving time were successfully solved on a computing cluster and in the volunteer computing project SAT@home. The solving time agrees well with estimations obtained by the proposed method.

On estimating total time to solve SAT in distributed computing environments: Application to the SAT@home project

This paper proposes a method to estimate the total time required to solve SAT in distributed environments via partitioning approach. It is based on the observation that for some simple forms of problem partitioning one can use the Monte Carlo approach to estimate the time required to solve an original problem. The method proposed is based on an algorithm for searching for partitioning with an optimal solving time estimation. We applied this method to estimate the time required to perform logical cryptanalysis of the widely known stream ciphers A5/1 and Bivium. The paper also describes a volunteer computing project SAT@home aimed at solving hard combinatorial problems reduced to SAT. In this project during several months there were solved 10 problems of logical cryptanalysis of the A5/1 cipher thatcould not be solved using known rainbow tables.