Using Monte Carlo method for searching partitionings of hard variants of Boolean satisfiability problem
Paper and Code
Jul 03, 2015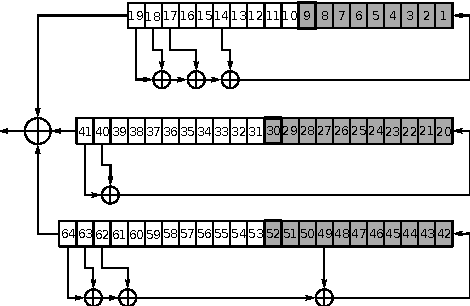
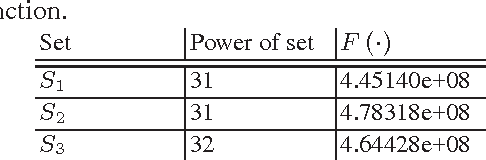
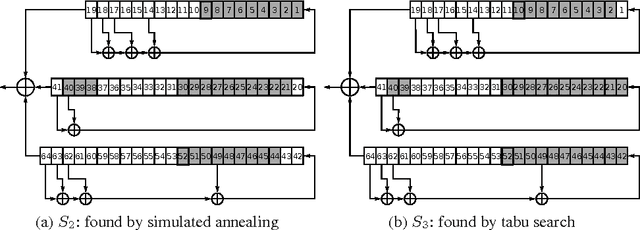

In this paper we propose the approach for constructing partitionings of hard variants of the Boolean satisfiability problem (SAT). Such partitionings can be used for solving corresponding SAT instances in parallel. For the same SAT instance one can construct different partitionings, each of them is a set of simplified versions of the original SAT instance. The effectiveness of an arbitrary partitioning is determined by the total time of solving of all SAT instances from it. We suggest the approach, based on the Monte Carlo method, for estimating time of processing of an arbitrary partitioning. With each partitioning we associate a point in the special finite search space. The estimation of effectiveness of the particular partitioning is the value of predictive function in the corresponding point of this space. The problem of search for an effective partitioning can be formulated as a problem of optimization of the predictive function. We use metaheuristic algorithms (simulated annealing and tabu search) to move from point to point in the search space. In our computational experiments we found partitionings for SAT instances encoding problems of inversion of some cryptographic functions. Several of these SAT instances with realistic predicted solving time were successfully solved on a computing cluster and in the volunteer computing project SAT@home. The solving time agrees well with estimations obtained by the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge