Oleg Filatov
Time Transfer: On Optimal Learning Rate and Batch Size In The Infinite Data Limit
Oct 08, 2024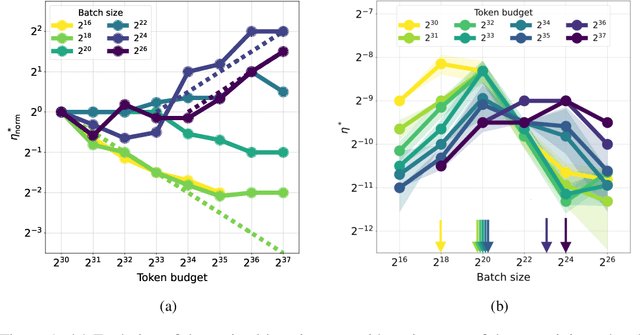
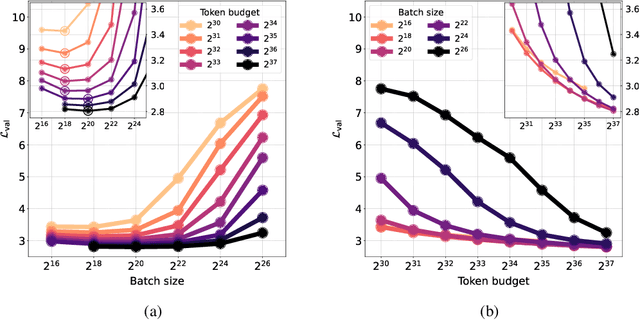
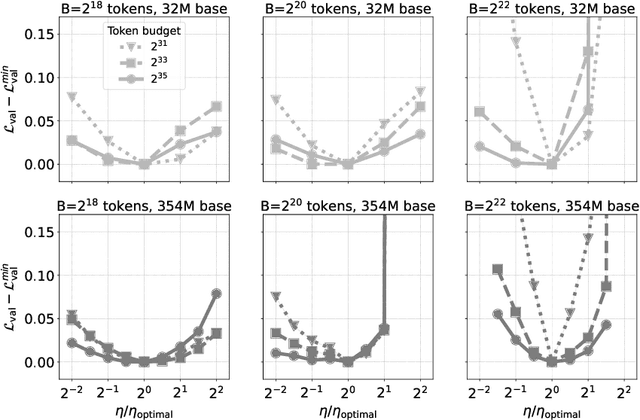
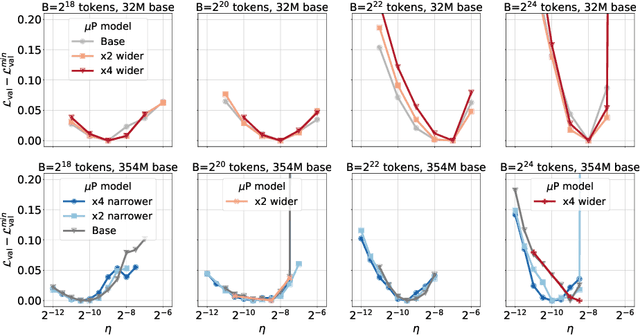
Abstract:One of the main challenges in optimal scaling of large language models (LLMs) is the prohibitive cost of hyperparameter tuning, particularly learning rate $\eta$ and batch size $B$. While techniques like $\mu$P (Yang et al., 2022) provide scaling rules for optimal $\eta$ transfer in the infinite model size limit, the optimal scaling behavior in the infinite data size limit ($T \to \infty$) remains unknown. We fill in this gap by observing for the first time an interplay of three optimal $\eta$ scaling regimes: $\eta \propto \sqrt{T}$, $\eta \propto 1$, and $\eta \propto 1/\sqrt{T}$ with transitions controlled by $B$ and its relation to the time-evolving critical batch size $B_\mathrm{crit} \propto T$. Furthermore, we show that the optimal batch size is positively correlated with $B_\mathrm{crit}$: keeping it fixed becomes suboptimal over time even if learning rate is scaled optimally. Surprisingly, our results demonstrate that the observed optimal $\eta$ and $B$ dynamics are preserved with $\mu$P model scaling, challenging the conventional view of $B_\mathrm{crit}$ dependence solely on loss value. Complementing optimality, we examine the sensitivity of loss to changes in learning rate, where we find the sensitivity to decrease with $T \to \infty$ and to remain constant with $\mu$P model scaling. We hope our results make the first step towards a unified picture of the joint optimal data and model scaling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge