Minibatch Optimal Transport and Perplexity Bound Estimation in Discrete Flow Matching

Outperforming autoregressive models on categorical data distributions, such as textual data, remains challenging for continuous diffusion and flow models. Discrete flow matching, a recent framework for modeling categorical data, has shown competitive performance with autoregressive models. Despite its similarities with continuous flow matching, the rectification strategy applied in the continuous version does not directly extend to the discrete one due to the inherent stochasticity of discrete paths. This limitation necessitates exploring alternative methods to minimize state transitions during generation. To address this, we propose a dynamic-optimal-transport-like minimization objective for discrete flows with convex interpolants and derive its equivalent Kantorovich formulation. The latter defines transport cost solely in terms of inter-state similarity and is optimized using a minibatch strategy. Another limitation we address in the discrete flow framework is model evaluation. Unlike continuous flows, wherein the instantaneous change of variables enables density estimation, discrete models lack a similar mechanism due to the inherent non-determinism and discontinuity of their paths. To alleviate this issue, we propose an upper bound on the perplexity of discrete flow models, enabling performance evaluation and comparison with other methods.

Blind Deinterleaving of Signals in Time Series with Self-attention Based Soft Min-cost Flow Learning

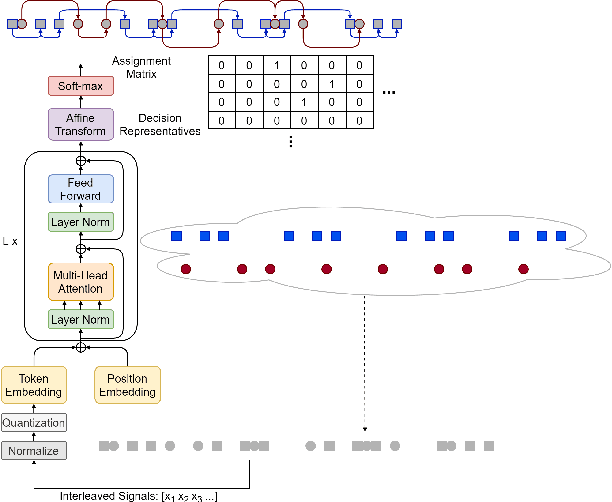
We propose an end-to-end learning approach to address deinterleaving of patterns in time series, in particular, radar signals. We link signal clustering problem to min-cost flow as an equivalent problem once the proper costs exist. We formulate a bi-level optimization problem involving min-cost flow as a sub-problem to learn such costs from the supervised training data. We then approximate the lower level optimization problem by self-attention based neural networks and provide a trainable framework that clusters the patterns in the input as the distinct flows. We evaluate our method with extensive experiments on a large dataset with several challenging scenarios to show the efficiency.

Deep Metric Learning with Alternating Projections onto Feasible Sets

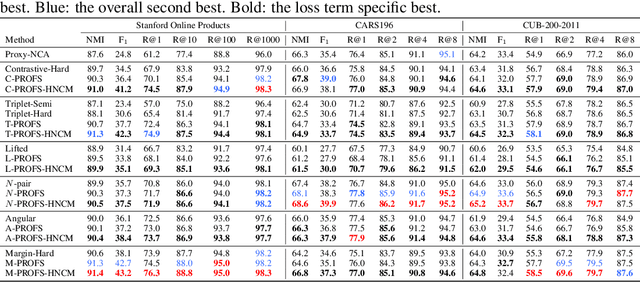
During the training of networks for distance metric learning, minimizers of the typical loss functions can be considered as "feasible points" satisfying a set of constraints imposed by the training data. To this end, we reformulate deep metric learning problem as finding a feasible point of a constraint set where the embedding vectors of the training data satisfy desired intra-class and inter-class proximity. The feasible set induced by the constraint set is expressed as the intersection of the relaxed feasible sets which enforce the proximity constraints only for particular samples (a sample from each class) of the training data. Then, the feasible point problem is to be approximately solved by performing alternating projections onto those feasible sets. Such an approach results in minimizing a typical loss function with a systematic batch set construction where these batches are constrained to contain the same sample from each class for a certain number of iterations. Moreover, these particular samples can be considered as the class representatives, allowing efficient utilization of hard class mining during batch construction. The proposed technique is applied with the contrastive, triplet, lifted structured, $N$-pair, angular and margin-based losses and evaluated on Stanford Online Products, CAR196 and CUB200-2011 datasets for image retrieval and clustering. The proposed approach outperforms state-of-the-art for all 6 loss functions with no additional computational cost and boosts its performance further by hard negative class mining.