Variational $f$-Divergence and Derangements for Discriminative Mutual Information Estimation

The accurate estimation of the mutual information is a crucial task in various applications, including machine learning, communications, and biology, since it enables the understanding of complex systems. High-dimensional data render the task extremely challenging due to the amount of data to be processed and the presence of convoluted patterns. Neural estimators based on variational lower bounds of the mutual information have gained attention in recent years but they are prone to either high bias or high variance as a consequence of the partition function. We propose a novel class of discriminative mutual information estimators based on the variational representation of the $f$-divergence. We investigate the impact of the permutation function used to obtain the marginal training samples and present a novel architectural solution based on derangements. The proposed estimator is flexible as it exhibits an excellent bias/variance trade-off. Experiments on reference scenarios demonstrate that our approach outperforms state-of-the-art neural estimators both in terms of accuracy and complexity.

Cooperative Channel Capacity Learning

In this paper, the problem of determining the capacity of a communication channel is formulated as a cooperative game, between a generator and a discriminator, that is solved via deep learning techniques. The task of the generator is to produce channel input samples for which the discriminator ideally distinguishes conditional from unconditional channel output samples. The learning approach, referred to as cooperative channel capacity learning (CORTICAL), provides both the optimal input signal distribution and the channel capacity estimate. Numerical results demonstrate that the proposed framework learns the capacity-achieving input distribution under challenging non-Shannon settings.

Copula Density Neural Estimation

Probability density estimation from observed data constitutes a central task in statistics. Recent advancements in machine learning offer new tools but also pose new challenges. The big data era demands analysis of long-range spatial and long-term temporal dependencies in large collections of raw data, rendering neural networks an attractive solution for density estimation. In this paper, we exploit the concept of copula to explicitly build an estimate of the probability density function associated to any observed data. In particular, we separate univariate marginal distributions from the joint dependence structure in the data, the copula itself, and we model the latter with a neural network-based method referred to as copula density neural estimation (CODINE). Results show that the novel learning approach is capable of modeling complex distributions and it can be applied for mutual information estimation and data generation.

MIND: Maximum Mutual Information Based Neural Decoder

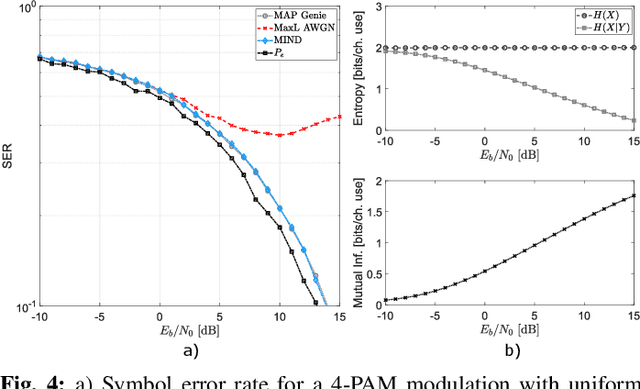
We are assisting at a growing interest in the development of learning architectures with application to digital communication systems. Herein, we consider the detection/decoding problem. We aim at developing an optimal neural architecture for such a task. The definition of the optimal criterion is a fundamental step. We propose to use the mutual information (MI) of the channel input-output signal pair. The computation of the MI is a formidable task, and for the majority of communication channels it is unknown. Therefore, the MI has to be learned. For such an objective, we propose a novel neural MI estimator based on a discriminative formulation. This leads to the derivation of the mutual information neural decoder (MIND). The developed neural architecture is capable not only to solve the decoding problem in unknown channels, but also to return an estimate of the average MI achieved with the coding scheme, as well as the decoding error probability. Several numerical results are reported and compared with maximum a-posteriori (MAP) and maximum likelihood (MaxL) decoding strategies.

Discriminative Mutual Information Estimation for the Design of Channel Capacity Driven Autoencoders

The development of optimal and efficient machine learning-based communication systems is likely to be a key enabler of beyond 5G communication technologies. In this direction, physical layer design has been recently reformulated under a deep learning framework where the autoencoder paradigm foresees the full communication system as an end-to-end coding-decoding problem. Given the loss function, the autoencoder jointly learns the coding and decoding optimal blocks under a certain channel model. Because performance in communications typically refers to achievable rates and channel capacity, the mutual information between channel input and output can be included in the end-to-end training process, thus, its estimation becomes essential. In this paper, we present a set of novel discriminative mutual information estimators and we discuss how to exploit them to design capacity-approaching codes and ultimately estimate the channel capacity.

Discriminative Mutual Information Estimators for Channel Capacity Learning

Channel capacity plays a crucial role in the development of modern communication systems as it represents the maximum rate at which information can be reliably transmitted over a communication channel. Nevertheless, for the majority of channels, finding a closed-form capacity expression remains an open challenge. This is because it requires to carry out two formidable tasks a) the computation of the mutual information between the channel input and output, and b) its maximization with respect to the signal distribution at the channel input. In this paper, we address both tasks. Inspired by implicit generative models, we propose a novel cooperative framework to automatically learn the channel capacity, for any type of memory-less channel. In particular, we firstly develop a new methodology to estimate the mutual information directly from a discriminator typically deployed to train adversarial networks, referred to as discriminative mutual information estimator (DIME). Secondly, we include the discriminator in a cooperative channel capacity learning framework, referred to as CORTICAL, where a discriminator learns to distinguish between dependent and independent channel input-output samples while a generator learns to produce the optimal channel input distribution for which the discriminator exhibits the best performance. Lastly, we prove that a particular choice of the cooperative value function solves the channel capacity estimation problem. Simulation results demonstrate that the proposed method offers high accuracy.

Capacity-Approaching Autoencoders for Communications

The autoencoder concept has fostered the reinterpretation and the design of modern communication systems. It consists of an encoder, a channel, and a decoder block which modify their internal neural structure in an end-to-end learning fashion. However, the current approach to train an autoencoder relies on the use of the cross-entropy loss function. This approach can be prone to overfitting issues and often fails to learn an optimal system and signal representation (code). In addition, less is known about the autoencoder ability to design channel capacity-approaching codes, i.e., codes that maximize the input-output information under a certain power constraint. The task being even more formidable for an unknown channel for which the capacity is unknown and therefore it has to be learnt. In this paper, we address the challenge of designing capacity-approaching codes by incorporating the presence of the communication channel into a novel loss function for the autoencoder training. In particular, we exploit the mutual information between the transmitted and received signals as a regularization term in the cross-entropy loss function, with the aim of controlling the amount of information stored. By jointly maximizing the mutual information and minimizing the cross-entropy, we propose a methodology that a) computes an estimate of the channel capacity and b) constructs an optimal coded signal approaching it. Several simulation results offer evidence of the potentiality of the proposed method.

Machine Learning Tips and Tricks for Power Line Communications

A great deal of attention has been recently given to Machine Learning (ML) techniques in many different application fields. This paper provides a vision of what ML can do in Power Line Communications (PLC). We firstly and briefly describe classical formulations of ML, and distinguish deterministic from statistical learning models with relevance to communications. We then discuss ML applications in PLC for each layer, namely, for characterization and modeling, for the development of physical layer algorithms, for media access control and networking. Finally, other applications of PLC that can benefit from the usage of ML, as grid diagnostics, are analyzed. Illustrative numerical examples are reported to serve the purpose of validating the ideas and motivate future research endeavors in this stimulating signal/data processing field.