On the Statistical Analysis of the Multipath Propagation Model Parameters for Power Line Communications

This paper proposes a fitting procedure that aims to identify the statistical properties of the parameters that describe the most widely known multipath propagation model (MPM) used in power line communication (PLC). Firstly, the MPM parameters are computed by fitting the theoretical model to a large database of single-input-single-output (SISO) experimental measurements, carried out in typical home premises. Secondly, the determined parameters are substituted back into the MPM formulation with the aim to prove their faithfulness, thus validating the proposed computation procedure. Then, the MPM parameters properties have been evaluated. In particular, the statistical behavior is established identifying the best fitting distribution by comparing the most common distributions through the use of the likelihood function. Moreover, the relationship among the different paths is highlighted in terms of statistical correlation. The identified statistical behavior for the MPM parameters confirms the assumptions of the previous works that, however, were mostly established in an heuristic way.

$f$-Divergence Based Classification: Beyond the Use of Cross-Entropy

In deep learning, classification tasks are formalized as optimization problems solved via the minimization of the cross-entropy. However, recent advancements in the design of objective functions allow the $f$-divergence measure to generalize the formulation of the optimization problem for classification. With this goal in mind, we adopt a Bayesian perspective and formulate the classification task as a maximum a posteriori probability problem. We propose a class of objective functions based on the variational representation of the $f$-divergence, from which we extract a list of five posterior probability estimators leveraging well-known $f$-divergences. In addition, driven by the challenge of improving the state-of-the-art approach, we propose a bottom-up method that leads us to the formulation of a new objective function (and posterior probability estimator) corresponding to a novel $f$-divergence referred to as shifted log (SL). First, we theoretically prove the convergence property of the posterior probability estimators. Then, we numerically test the set of proposed objective functions in three application scenarios: toy examples, image data sets, and signal detection/decoding problems. The analyzed tasks demonstrate the effectiveness of the proposed estimators and that the SL divergence achieves the highest classification accuracy in almost all the scenarios.

Destination Scheduling for Secure Pinhole-Based Power-Line Communication

We propose an optimal destination scheduling scheme to improve the physical layer security (PLS) of a power-line communication (PLC) based Internet-of-Things system in the presence of an eavesdropper. We consider a pinhole (PH) architecture for a multi-node PLC network to capture the keyhole effect in PLC. The transmitter-to-PH link is shared between the destinations and an eavesdropper which correlates all end-to-end links. The individual channel gains are assumed to follow independent log-normal statistics. Furthermore, the additive impulsive noise at each node is modeled by an independent Bernoulli-Gaussian process. Exact computable expressions for the average secrecy capacity (ASC) and the probability of intercept (POI) performance over many different networks are derived. Approximate closed-form expressions for the asymptotic ASC and POI are also provided. We find that the asymptotic ASC saturates to a constant level as transmit power increases. We observe that the PH has an adverse effect on the ASC. Although the shared link affects the ASC, it has no effect on the POI. We show that by artificially controlling the impulsive to background noise power ratio and its arrival rate at the receivers, the secrecy performance can be improved.

Variational $f$-Divergence and Derangements for Discriminative Mutual Information Estimation

The accurate estimation of the mutual information is a crucial task in various applications, including machine learning, communications, and biology, since it enables the understanding of complex systems. High-dimensional data render the task extremely challenging due to the amount of data to be processed and the presence of convoluted patterns. Neural estimators based on variational lower bounds of the mutual information have gained attention in recent years but they are prone to either high bias or high variance as a consequence of the partition function. We propose a novel class of discriminative mutual information estimators based on the variational representation of the $f$-divergence. We investigate the impact of the permutation function used to obtain the marginal training samples and present a novel architectural solution based on derangements. The proposed estimator is flexible as it exhibits an excellent bias/variance trade-off. Experiments on reference scenarios demonstrate that our approach outperforms state-of-the-art neural estimators both in terms of accuracy and complexity.

Cooperative Channel Capacity Learning

In this paper, the problem of determining the capacity of a communication channel is formulated as a cooperative game, between a generator and a discriminator, that is solved via deep learning techniques. The task of the generator is to produce channel input samples for which the discriminator ideally distinguishes conditional from unconditional channel output samples. The learning approach, referred to as cooperative channel capacity learning (CORTICAL), provides both the optimal input signal distribution and the channel capacity estimate. Numerical results demonstrate that the proposed framework learns the capacity-achieving input distribution under challenging non-Shannon settings.

An Asymptotically Equivalent GLRT Test for Distributed Detection in Wireless Sensor Networks

In this article, we consider the problem of distributed detection of a localized radio source emitting a signal. We consider that geographically distributed sensor nodes obtain energy measurements and compute cooperatively a statistic to decide if the source is present or absent. We model the radio source as a stochastic signal and deal with spatially statistically dependent measurements, whose probability density function (PDF) has unknown positive parameters when the radio source is active. Under the framework of the Generalized Likelihood Ratio Test (GLRT) theory, the positive constraint on the unknown multidimensional parameter makes the computation of the GLRT asymptotic performance (when the amount of sensor measurements tends to infinity) more involved. Nevertheless, we analytically characterize the asymptotic distribution of the statistic. Moreover, as the GLRT is not amenable for distributed settings because of the spatial statistical dependence of the measurements, we study a GLRT-like test where the joint PDF of the measurements is substituted by the product of its marginal PDFs, and therefore, the statistical dependence is completely discarded for building this test. Nevertheless, its asymptotic performance is proved to be identical to the original GLRT, showing that the statistically dependence of the measurements has no impact on the detection performance in the asymptotic scenario. Furthermore, the GLRT-like algorithm has a low computational complexity and demands low communication resources, as compared to the GLRT.

Copula Density Neural Estimation

Probability density estimation from observed data constitutes a central task in statistics. Recent advancements in machine learning offer new tools but also pose new challenges. The big data era demands analysis of long-range spatial and long-term temporal dependencies in large collections of raw data, rendering neural networks an attractive solution for density estimation. In this paper, we exploit the concept of copula to explicitly build an estimate of the probability density function associated to any observed data. In particular, we separate univariate marginal distributions from the joint dependence structure in the data, the copula itself, and we model the latter with a neural network-based method referred to as copula density neural estimation (CODINE). Results show that the novel learning approach is capable of modeling complex distributions and it can be applied for mutual information estimation and data generation.

An Exponentially-Tight Approximate Factorization of the Joint PDF of Statistical Dependent Measurements in Wireless Sensor Networks

We consider the distributed detection problem of a temporally correlated random radio source signal using a wireless sensor network capable of measuring the energy of the received signals. It is well-known that optimal tests in the Neyman-Pearson setting are based on likelihood ratio tests (LRT), which, in this set-up, evaluate the quotient between the probability density functions (PDF) of the measurements when the source signal is present and absent. When the source is present, the computation of the joint PDF of the energy measurements at the nodes is a challenging problem. This is due to the statistical dependence introduced to the received signals by the radio source propagated through fading channels. We deal with this problem using the characteristic function of the (intractable) joint PDF, and proposing an approximation to it. We derive bounds for the approximation error in two wireless propagation scenarios, slow and fast fading, and show that the proposed approximation is exponentially tight with the number of nodes when the time-bandwidth product is sufficiently high. The approximation is used as a substitute of the exact joint PDF for building an approximate LRT, which performs better than other well-known detectors, as verified by Monte Carlo simulations.

MIND: Maximum Mutual Information Based Neural Decoder

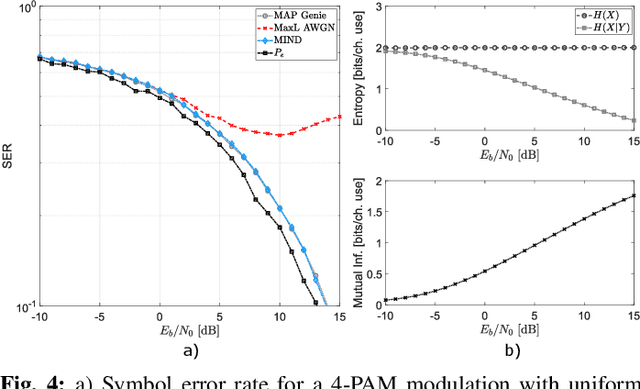
We are assisting at a growing interest in the development of learning architectures with application to digital communication systems. Herein, we consider the detection/decoding problem. We aim at developing an optimal neural architecture for such a task. The definition of the optimal criterion is a fundamental step. We propose to use the mutual information (MI) of the channel input-output signal pair. The computation of the MI is a formidable task, and for the majority of communication channels it is unknown. Therefore, the MI has to be learned. For such an objective, we propose a novel neural MI estimator based on a discriminative formulation. This leads to the derivation of the mutual information neural decoder (MIND). The developed neural architecture is capable not only to solve the decoding problem in unknown channels, but also to return an estimate of the average MI achieved with the coding scheme, as well as the decoding error probability. Several numerical results are reported and compared with maximum a-posteriori (MAP) and maximum likelihood (MaxL) decoding strategies.

Discriminative Mutual Information Estimation for the Design of Channel Capacity Driven Autoencoders

The development of optimal and efficient machine learning-based communication systems is likely to be a key enabler of beyond 5G communication technologies. In this direction, physical layer design has been recently reformulated under a deep learning framework where the autoencoder paradigm foresees the full communication system as an end-to-end coding-decoding problem. Given the loss function, the autoencoder jointly learns the coding and decoding optimal blocks under a certain channel model. Because performance in communications typically refers to achievable rates and channel capacity, the mutual information between channel input and output can be included in the end-to-end training process, thus, its estimation becomes essential. In this paper, we present a set of novel discriminative mutual information estimators and we discuss how to exploit them to design capacity-approaching codes and ultimately estimate the channel capacity.