Reproducible Machine Learning-based Voice Pathology Detection: Introducing the Pitch Difference Feature

In this study, we propose a robust set of features derived from a thorough research of contemporary practices in voice pathology detection. The feature set is based on the combination of acoustic handcrafted features. Additionally, we introduce pitch difference as a novel feature. We combine this feature set, containing data from the publicly available Saarbr\"ucken Voice Database (SVD), with preprocessing using the K-Means Synthetic Minority Over-Sampling Technique algorithm to address class imbalance. Moreover, we applied multiple ML models as binary classifiers. We utilized support vector machine, k-nearest neighbors, naive Bayes, decision tree, random forest and AdaBoost classifiers. To determine the best classification approach, we performed grid search on feasible hyperparameters of respective classifiers and subsections of features. Our approach has achieved the state-of-the-art performance, measured by unweighted average recall in voice pathology detection on SVD database. We intentionally omit accuracy as it is highly biased metric in case of unbalanced data compared to aforementioned metrics. The results are further enhanced by eliminating the potential overestimation of the results with repeated stratified cross-validation. This advancement demonstrates significant potential for the clinical deployment of ML methods, offering a valuable tool for an objective examination of voice pathologies. To support our claims, we provide a publicly available GitHub repository with DOI 10.5281/zenodo.13771573. Finally, we provide REFORMS checklist.

A Letter on Convergence of In-Parameter-Linear Nonlinear Neural Architectures with Gradient Learnings

This letter summarizes and proves the concept of bounded-input bounded-state (BIBS) stability for weight convergence of a broad family of in-parameter-linear nonlinear neural architectures as it generally applies to a broad family of incremental gradient learning algorithms. A practical BIBS convergence condition results from the derived proofs for every individual learning point or batches for real-time applications.

An Approach to Stable Gradient Descent Adaptation of Higher-Order Neural Units

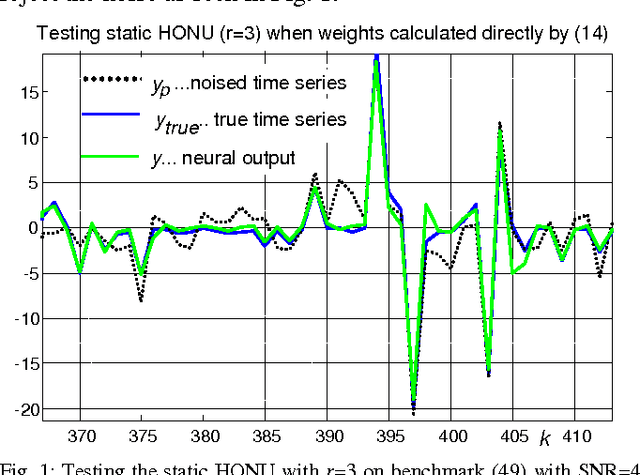
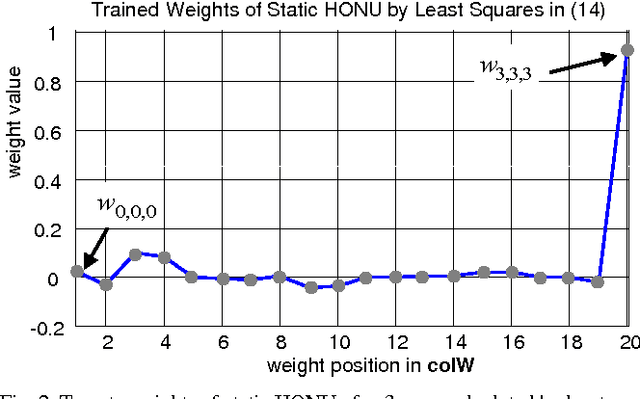
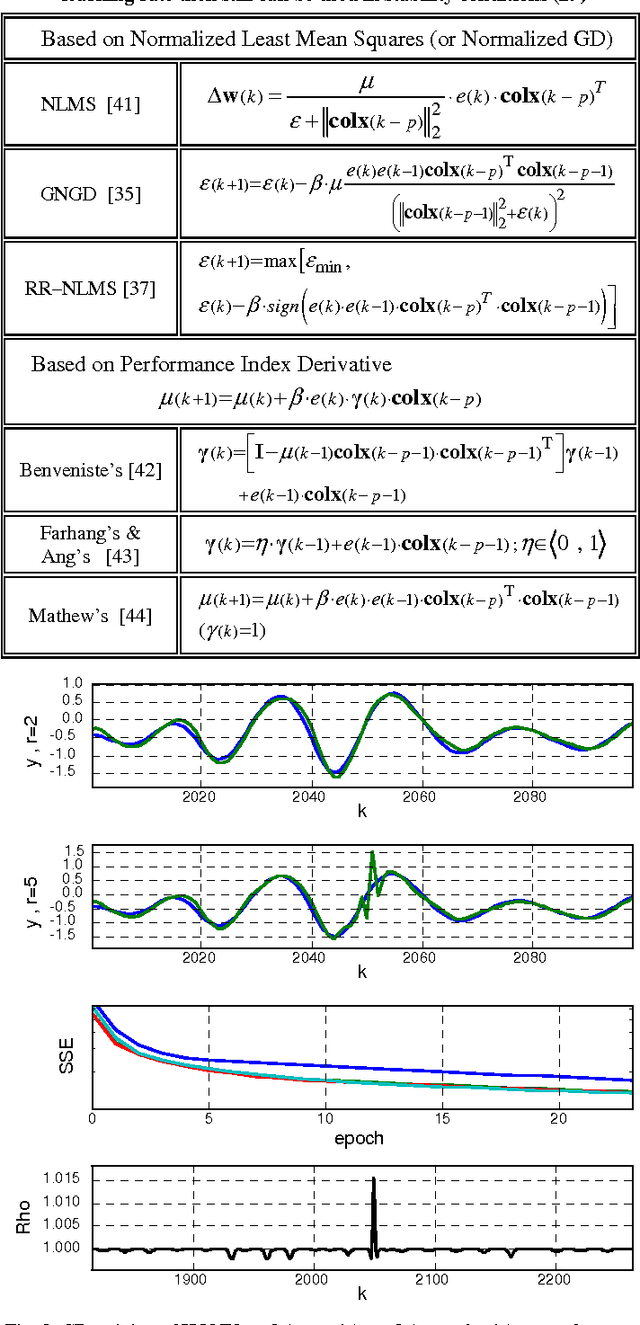
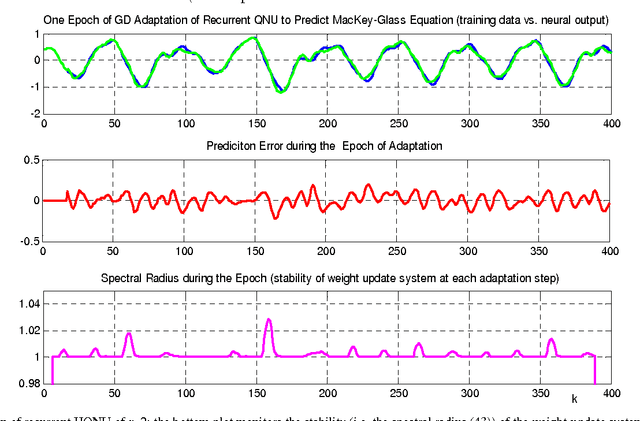
Stability evaluation of a weight-update system of higher-order neural units (HONUs) with polynomial aggregation of neural inputs (also known as classes of polynomial neural networks) for adaptation of both feedforward and recurrent HONUs by a gradient descent method is introduced. An essential core of the approach is based on spectral radius of a weight-update system, and it allows stability monitoring and its maintenance at every adaptation step individually. Assuring stability of the weight-update system (at every single adaptation step) naturally results in adaptation stability of the whole neural architecture that adapts to target data. As an aside, the used approach highlights the fact that the weight optimization of HONU is a linear problem, so the proposed approach can be generally extended to any neural architecture that is linear in its adaptable parameters.