An Approach to Stable Gradient Descent Adaptation of Higher-Order Neural Units
Paper and Code
Jun 23, 2016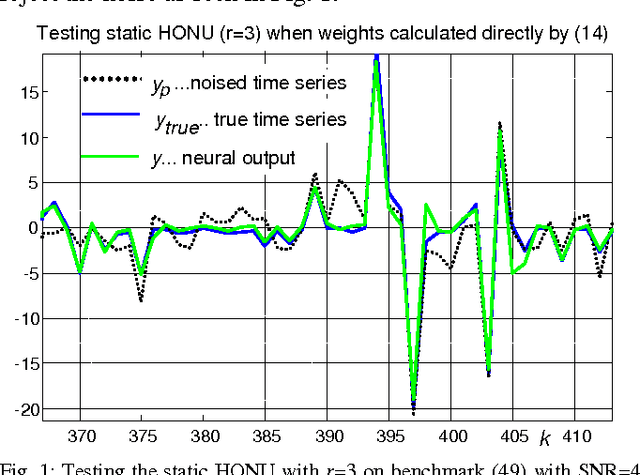
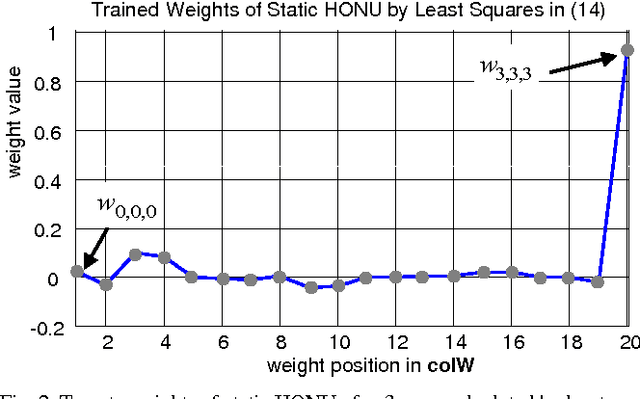
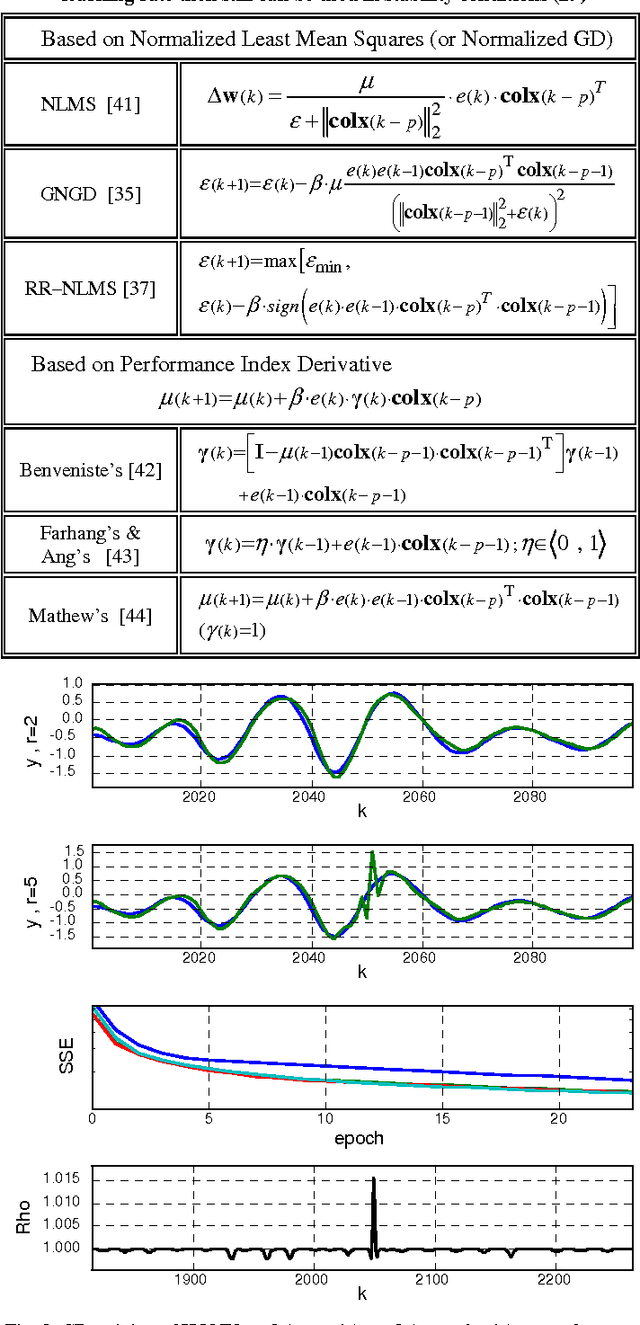
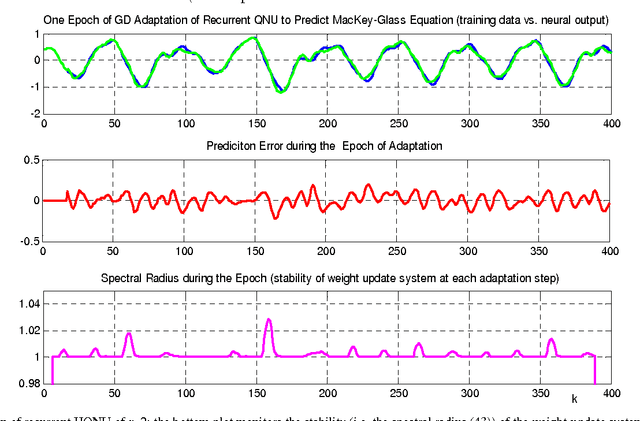
Stability evaluation of a weight-update system of higher-order neural units (HONUs) with polynomial aggregation of neural inputs (also known as classes of polynomial neural networks) for adaptation of both feedforward and recurrent HONUs by a gradient descent method is introduced. An essential core of the approach is based on spectral radius of a weight-update system, and it allows stability monitoring and its maintenance at every adaptation step individually. Assuring stability of the weight-update system (at every single adaptation step) naturally results in adaptation stability of the whole neural architecture that adapts to target data. As an aside, the used approach highlights the fact that the weight optimization of HONU is a linear problem, so the proposed approach can be generally extended to any neural architecture that is linear in its adaptable parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge