Analyzing Echo-state Networks Using Fractal Dimension

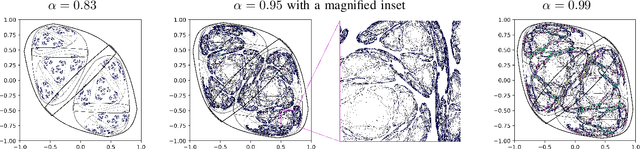
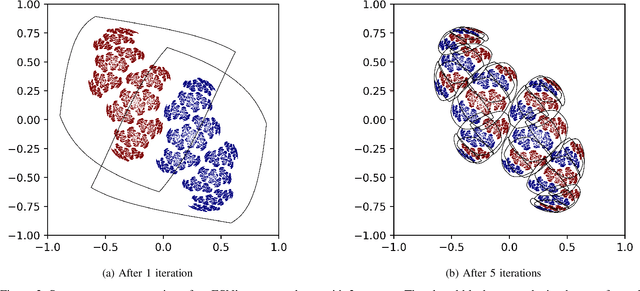
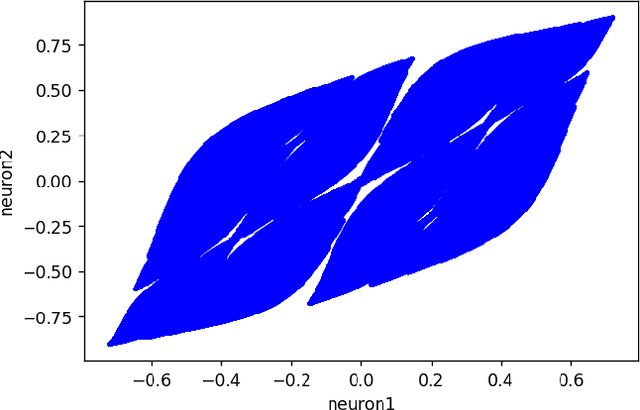
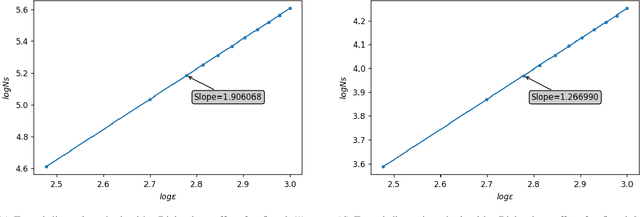
This work joins aspects of reservoir optimization, information-theoretic optimal encoding, and at its center fractal analysis. We build on the observation that, due to the recursive nature of recurrent neural networks, input sequences appear as fractal patterns in their hidden state representation. These patterns have a fractal dimension that is lower than the number of units in the reservoir. We show potential usage of this fractal dimension with regard to optimization of recurrent neural network initialization. We connect the idea of `ideal' reservoirs to lossless optimal encoding using arithmetic encoders. Our investigation suggests that the fractal dimension of the mapping from input to hidden state shall be close to the number of units in the network. This connection between fractal dimension and network connectivity is an interesting new direction for recurrent neural network initialization and reservoir computing.

Kinematics and dynamics of an egg-shaped robot with a gyro driven inertia actuator

The manuscript discusses still preliminary considerations with regard to the dynamics and kinematics of an egg shaped robot with an gyro driven inertia actuator. The method of calculation follows the idea that we would like to express the entire dynamic equations in terms of moments instead of forces. Also we avoid to derive the equations from a Lagrange function with constraints. The result of the calculations is meant to be applicable to two robot prototypes that have been build at the AES\&R Laboratory at the National Chung Cheng University in Taiwan.

Orthogonal Echo State Networks and stochastic evaluations of likelihoods

We report about probabilistic likelihood estimates that are performed on time series using an echo state network with orthogonal recurrent connectivity. The results from tests using synthetic stochastic input time series with temporal inference indicate that the capability of the network to infer depends on the balance between input strength and recurrent activity. This balance has an influence on the network with regard to the quality of inference from the short term input history versus inference that accounts for influences that date back a long time. Sensitivity of such networks against noise and the finite accuracy of network states in the recurrent layer are investigated. In addition, a measure based on mutual information between the output time series and the reservoir is introduced. Finally, different types of recurrent connectivity are evaluated. Orthogonal matrices show the best results of all investigated connectivity types overall, but also in the way how the network performance scales with the size of the recurrent layer.

Critical Echo State Networks that Anticipate Input using Morphable Transfer Functions

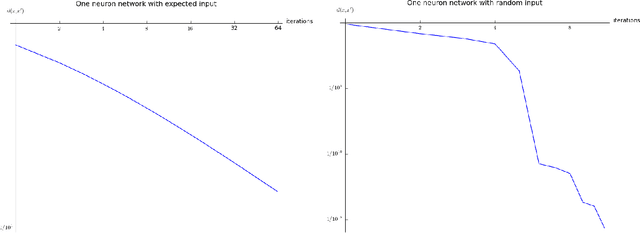
The paper investigates a new type of truly critical echo state networks where individual transfer functions for every neuron can be modified to anticipate the expected next input. Deviations from expected input are only forgotten slowly in power law fashion. The paper outlines the theory, numerically analyzes a one neuron model network and finally discusses technical and also biological implications of this type of approach.

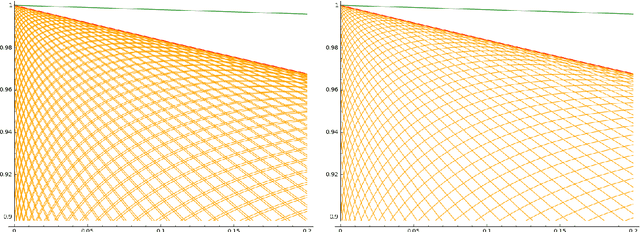
Echo State Condition at the Critical Point

Recurrent networks with transfer functions that fulfill the Lipschitz continuity with K=1 may be echo state networks if certain limitations on the recurrent connectivity are applied. It has been shown that it is sufficient if the largest singular value of the recurrent connectivity is smaller than 1. The main achievement of this paper is a proof under which conditions the network is an echo state network even if the largest singular value is one. It turns out that in this critical case the exact shape of the transfer function plays a decisive role in determining whether the network still fulfills the echo state condition. In addition, several examples with one neuron networks are outlined to illustrate effects of critical connectivity. Moreover, within the manuscript a mathematical definition for a critical echo state network is suggested.

Input anticipating critical reservoirs show power law forgetting of unexpected input events

Usually, reservoir computing shows an exponential memory decay. This paper investigates under which circumstances echo state networks can show a power law forgetting. That means traces of earlier events can be found in the reservoir for very long time spans. Such a setting requires critical connectivity exactly at the limit of what is permissible according the echo state condition. However, for general matrices the limit cannot be determined exactly from theory. In addition, the behavior of the network is strongly influenced by the input flow. Results are presented that use certain types of restricted recurrent connectivity and anticipation learning with regard to the input, where indeed power law forgetting can be achieved.