Analyzing Echo-state Networks Using Fractal Dimension
Paper and Code
May 26, 2022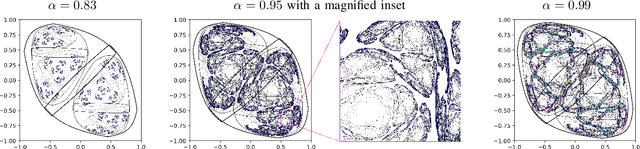
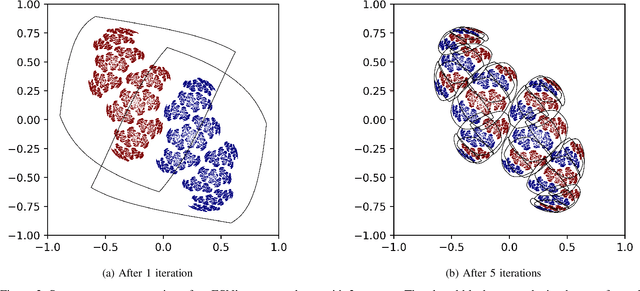
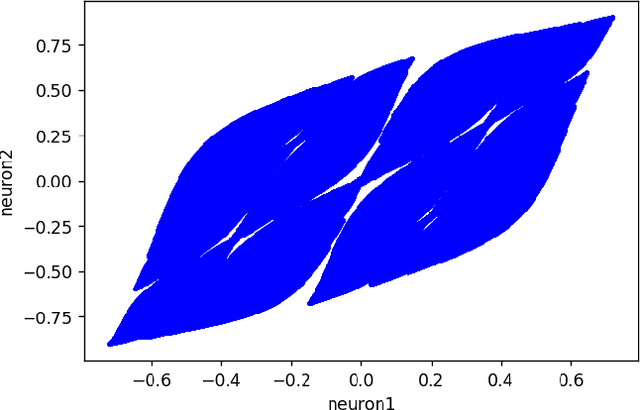
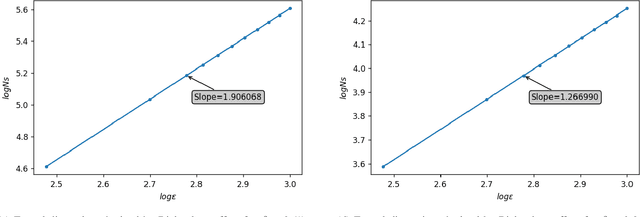
This work joins aspects of reservoir optimization, information-theoretic optimal encoding, and at its center fractal analysis. We build on the observation that, due to the recursive nature of recurrent neural networks, input sequences appear as fractal patterns in their hidden state representation. These patterns have a fractal dimension that is lower than the number of units in the reservoir. We show potential usage of this fractal dimension with regard to optimization of recurrent neural network initialization. We connect the idea of `ideal' reservoirs to lossless optimal encoding using arithmetic encoders. Our investigation suggests that the fractal dimension of the mapping from input to hidden state shall be close to the number of units in the network. This connection between fractal dimension and network connectivity is an interesting new direction for recurrent neural network initialization and reservoir computing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge