Echo State Condition at the Critical Point

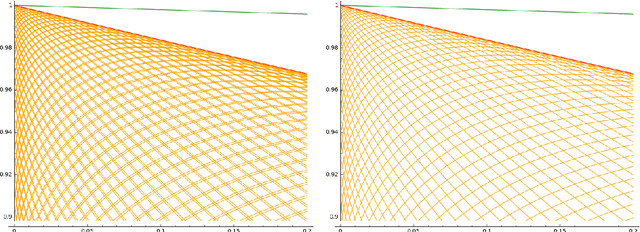
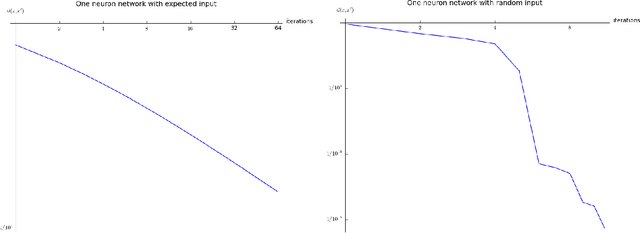
Recurrent networks with transfer functions that fulfill the Lipschitz continuity with K=1 may be echo state networks if certain limitations on the recurrent connectivity are applied. It has been shown that it is sufficient if the largest singular value of the recurrent connectivity is smaller than 1. The main achievement of this paper is a proof under which conditions the network is an echo state network even if the largest singular value is one. It turns out that in this critical case the exact shape of the transfer function plays a decisive role in determining whether the network still fulfills the echo state condition. In addition, several examples with one neuron networks are outlined to illustrate effects of critical connectivity. Moreover, within the manuscript a mathematical definition for a critical echo state network is suggested.