Nishant Vijayakumar
Risk Aware Ranking for Top-$k$ Recommendations
Apr 12, 2019
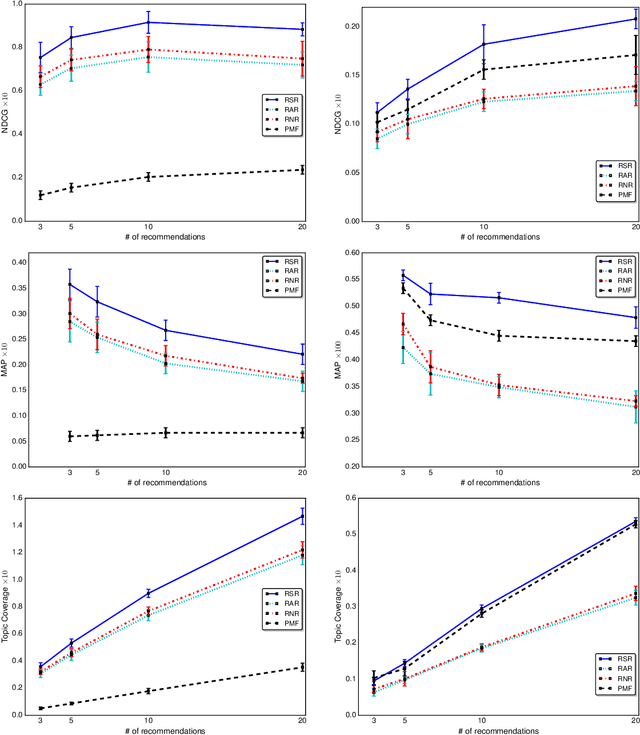
Abstract:Given an incomplete ratings data over a set of users and items, the preference completion problem aims to estimate a personalized total preference order over a subset of the items. In practical settings, a ranked list of top-$k$ items from the estimated preference order is recommended to the end user in the decreasing order of preference for final consumption. We analyze this model and observe that such a ranking model results in suboptimal performance when the payoff associated with the recommended items is different. We propose a novel and very efficient algorithm for the preference ranking considering the uncertainty regarding the payoffs of the items. Once the preference scores for the users are obtained using any preference learning algorithm, we show that ranking the items using a risk seeking utility function results in the best ranking performance.
SAGA: A Submodular Greedy Algorithm For Group Recommendation
Dec 25, 2017



Abstract:In this paper, we propose a unified framework and an algorithm for the problem of group recommendation where a fixed number of items or alternatives can be recommended to a group of users. The problem of group recommendation arises naturally in many real world contexts, and is closely related to the budgeted social choice problem studied in economics. We frame the group recommendation problem as choosing a subgraph with the largest group consensus score in a completely connected graph defined over the item affinity matrix. We propose a fast greedy algorithm with strong theoretical guarantees, and show that the proposed algorithm compares favorably to the state-of-the-art group recommendation algorithms according to commonly used relevance and coverage performance measures on benchmark dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge