Sample and Map from a Single Convex Potential: Generation using Conjugate Moment Measures

A common approach to generative modeling is to split model-fitting into two blocks: define first how to sample noise (e.g. Gaussian) and choose next what to do with it (e.g. using a single map or flows). We explore in this work an alternative route that ties sampling and mapping. We find inspiration in moment measures, a result that states that for any measure $\rho$ supported on a compact convex set of $\mathbb{R}^d$, there exists a unique convex potential $u$ such that $\rho=\nabla u\,\sharp\,e^{-u}$. While this does seem to tie effectively sampling (from log-concave distribution $e^{-u}$) and action (pushing particles through $\nabla u$), we observe on simple examples (e.g., Gaussians or 1D distributions) that this choice is ill-suited for practical tasks. We study an alternative factorization, where $\rho$ is factorized as $\nabla w^*\,\sharp\,e^{-w}$, where $w^*$ is the convex conjugate of $w$. We call this approach conjugate moment measures, and show far more intuitive results on these examples. Because $\nabla w^*$ is the Monge map between the log-concave distribution $e^{-w}$ and $\rho$, we rely on optimal transport solvers to propose an algorithm to recover $w$ from samples of $\rho$, and parameterize $w$ as an input-convex neural network.

On a Neural Implementation of Brenier's Polar Factorization

In 1991, Brenier proved a theorem that generalizes the $QR$ decomposition for square matrices -- factored as PSD $\times$ unitary -- to any vector field $F:\mathbb{R}^d\rightarrow \mathbb{R}^d$. The theorem, known as the polar factorization theorem, states that any field $F$ can be recovered as the composition of the gradient of a convex function $u$ with a measure-preserving map $M$, namely $F=\nabla u \circ M$. We propose a practical implementation of this far-reaching theoretical result, and explore possible uses within machine learning. The theorem is closely related to optimal transport (OT) theory, and we borrow from recent advances in the field of neural optimal transport to parameterize the potential $u$ as an input convex neural network. The map $M$ can be either evaluated pointwise using $u^*$, the convex conjugate of $u$, through the identity $M=\nabla u^* \circ F$, or learned as an auxiliary network. Because $M$ is, in general, not injective, we consider the additional task of estimating the ill-posed inverse map that can approximate the pre-image measure $M^{-1}$ using a stochastic generator. We illustrate possible applications of \citeauthor{Brenier1991PolarFA}'s polar factorization to non-convex optimization problems, as well as sampling of densities that are not log-concave.

Deep Neural Networks Are Congestion Games: From Loss Landscape to Wardrop Equilibrium and Beyond

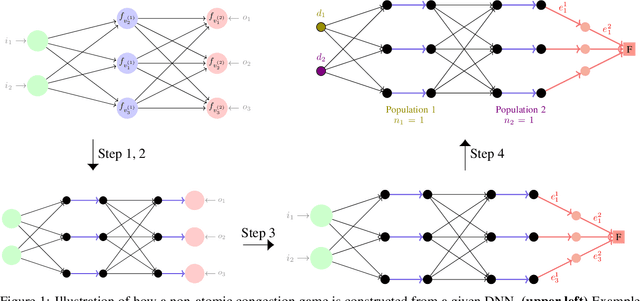
The theoretical analysis of deep neural networks (DNN) is arguably among the most challenging research directions in machine learning (ML) right now, as it requires from scientists to lay novel statistical learning foundations to explain their behaviour in practice. While some success has been achieved recently in this endeavour, the question on whether DNNs can be analyzed using the tools from other scientific fields outside the ML community has not received the attention it may well have deserved. In this paper, we explore the interplay between DNNs and game theory (GT), and show how one can benefit from the classic readily available results from the latter when analyzing the former. In particular, we consider the widely studied class of congestion games, and illustrate their intrinsic relatedness to both linear and non-linear DNNs and to the properties of their loss surface. Beyond retrieving the state-of-the-art results from the literature, we argue that our work provides a very promising novel tool for analyzing the DNNs and support this claim by proposing concrete open problems that can advance significantly our understanding of DNNs when solved.