Interpretable Vision Transformers in Image Classification via SVDA

Vision Transformers (ViTs) have achieved state-of-the-art performance in image classification, yet their attention mechanisms often remain opaque and exhibit dense, non-structured behaviors. In this work, we adapt our previously proposed SVD-Inspired Attention (SVDA) mechanism to the ViT architecture, introducing a geometrically grounded formulation that enhances interpretability, sparsity, and spectral structure. We apply the use of interpretability indicators -- originally proposed with SVDA -- to monitor attention dynamics during training and assess structural properties of the learned representations. Experimental evaluations on four widely used benchmarks -- CIFAR-10, FashionMNIST, CIFAR-100, and ImageNet-100 -- demonstrate that SVDA consistently yields more interpretable attention patterns without sacrificing classification accuracy. While the current framework offers descriptive insights rather than prescriptive guidance, our results establish SVDA as a comprehensive and informative tool for analyzing and developing structured attention models in computer vision. This work lays the foundation for future advances in explainable AI, spectral diagnostics, and attention-based model compression.

Interpretable Vision Transformers in Monocular Depth Estimation via SVDA

Monocular depth estimation is a central problem in computer vision with applications in robotics, AR, and autonomous driving, yet the self-attention mechanisms that drive modern Transformer architectures remain opaque. We introduce SVD-Inspired Attention (SVDA) into the Dense Prediction Transformer (DPT), providing the first spectrally structured formulation of attention for dense prediction tasks. SVDA decouples directional alignment from spectral modulation by embedding a learnable diagonal matrix into normalized query-key interactions, enabling attention maps that are intrinsically interpretable rather than post-hoc approximations. Experiments on KITTI and NYU-v2 show that SVDA preserves or slightly improves predictive accuracy while adding only minor computational overhead. More importantly, SVDA unlocks six spectral indicators that quantify entropy, rank, sparsity, alignment, selectivity, and robustness. These reveal consistent cross-dataset and depth-wise patterns in how attention organizes during training, insights that remain inaccessible in standard Transformers. By shifting the role of attention from opaque mechanism to quantifiable descriptor, SVDA redefines interpretability in monocular depth estimation and opens a principled avenue toward transparent dense prediction models.

Towards Explainability in Monocular Depth Estimation

The estimation of depth in two-dimensional images has long been a challenging and extensively studied subject in computer vision. Recently, significant progress has been made with the emergence of Deep Learning-based approaches, which have proven highly successful. This paper focuses on the explainability in monocular depth estimation methods, in terms of how humans perceive depth. This preliminary study emphasizes on one of the most significant visual cues, the relative size, which is prominent in almost all viewed images. We designed a specific experiment to mimic the experiments in humans and have tested state-of-the-art methods to indirectly assess the explainability in the context defined. In addition, we observed that measuring the accuracy required further attention and a particular approach is proposed to this end. The results show that a mean accuracy of around 77% across methods is achieved, with some of the methods performing markedly better, thus, indirectly revealing their corresponding potential to uncover monocular depth cues, like relative size.

Salt-n-pepper noise filtering using Cellular Automata

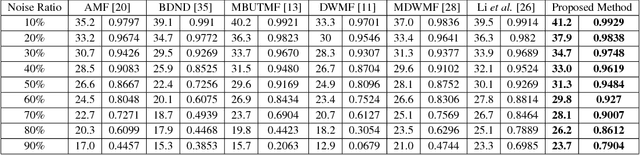
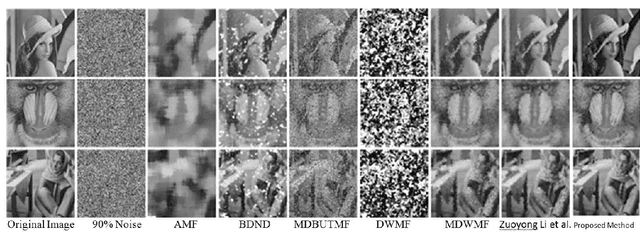
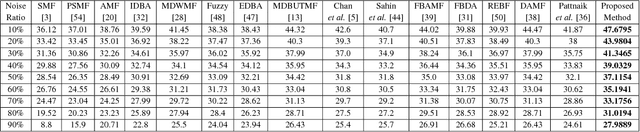
Cellular Automata (CA) have been considered one of the most pronounced parallel computational tools in the recent era of nature and bio-inspired computing. Taking advantage of their local connectivity, the simplicity of their design and their inherent parallelism, CA can be effectively applied to many image processing tasks. In this paper, a CA approach for efficient salt-n-pepper noise filtering in grayscale images is presented. Using a 2D Moore neighborhood, the classified "noisy" cells are corrected by averaging the non-noisy neighboring cells. While keeping the computational burden really low, the proposed approach succeeds in removing high-noise levels from various images and yields promising qualitative and quantitative results, compared to state-of-the-art techniques.

A Generalised Directional Laplacian Distribution: Estimation, Mixture Models and Audio Source Separation

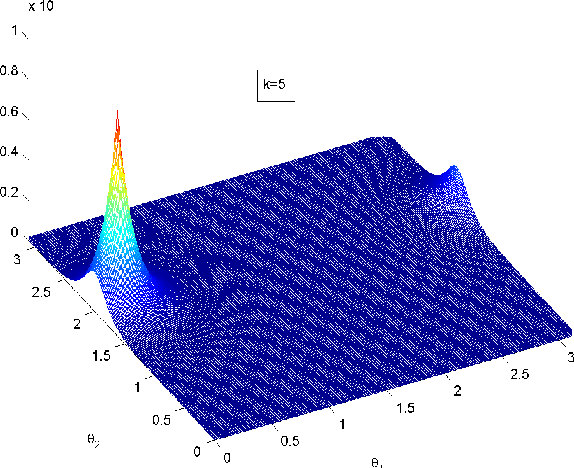
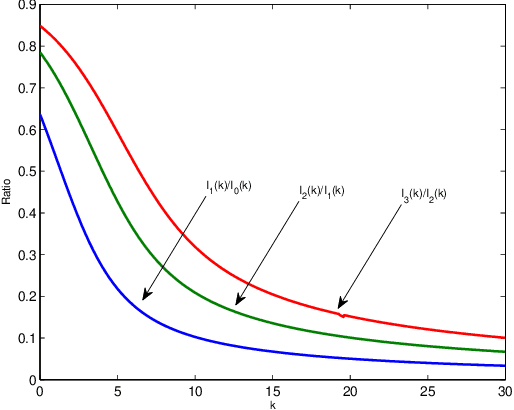
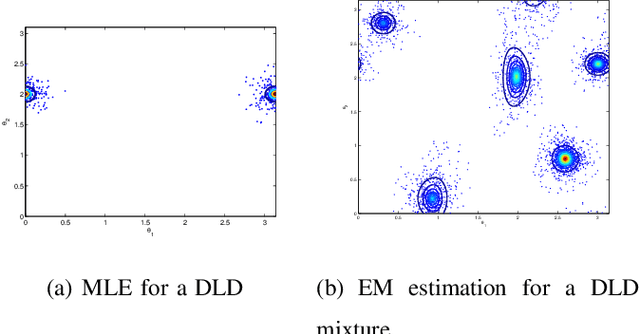
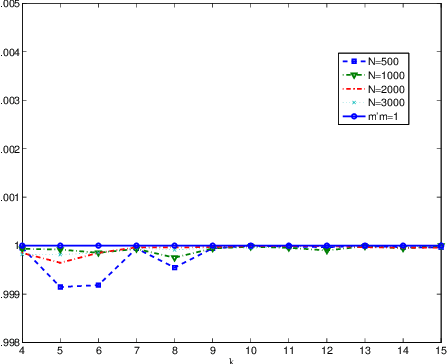
Directional or Circular statistics are pertaining to the analysis and interpretation of directions or rotations. In this work, a novel probability distribution is proposed to model multidimensional sparse directional data. The Generalised Directional Laplacian Distribution (DLD) is a hybrid between the Laplacian distribution and the von Mises-Fisher distribution. The distribution's parameters are estimated using Maximum-Likelihood Estimation over a set of training data points. Mixtures of Directional Laplacian Distributions (MDLD) are also introduced in order to model multiple concentrations of sparse directional data. The author explores the application of the derived DLD mixture model to cluster sound sources that exist in an underdetermined instantaneous sound mixture. The proposed model can solve the general K x L (K<L) underdetermined instantaneous source separation problem, offering a fast and stable solution.

Convolutive Audio Source Separation using Robust ICA and an intelligent evolving permutation ambiguity solution

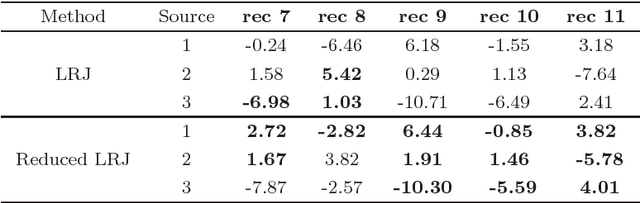
Audio source separation is the task of isolating sound sources that are active simultaneously in a room captured by a set of microphones. Convolutive audio source separation of equal number of sources and microphones has a number of shortcomings including the complexity of frequency-domain ICA, the permutation ambiguity and the problem's scalabity with increasing number of sensors. In this paper, the authors propose a multiple-microphone audio source separation algorithm based on a previous work of Mitianoudis and Davies (2003). Complex FastICA is substituted by Robust ICA increasing robustness and performance. Permutation ambiguity is solved using two methodologies. The first is using the Likelihood Ration Jump solution, which is now modified to decrease computational complexity in the case of multiple microphones. The application of the MuSIC algorithm, as a preprocessing step to the previous solution, forms a second methodology with promising results.