Budget-Constrained Bounds for Mini-Batch Estimation of Optimal Transport

Optimal Transport (OT) is a fundamental tool for comparing probability distributions, but its exact computation remains prohibitive for large datasets. In this work, we introduce novel families of upper and lower bounds for the OT problem constructed by aggregating solutions of mini-batch OT problems. The upper bound family contains traditional mini-batch averaging at one extreme and a tight bound found by optimal coupling of mini-batches at the other. In between these extremes, we propose various methods to construct bounds based on a fixed computational budget. Through various experiments, we explore the trade-off between computational budget and bound tightness and show the usefulness of these bounds in computer vision applications.

Initialization and Regularization of Factorized Neural Layers

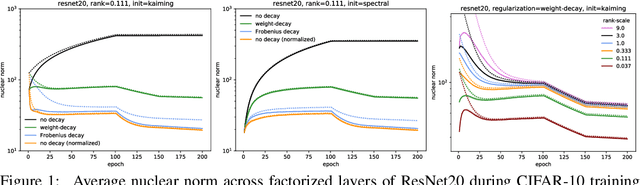
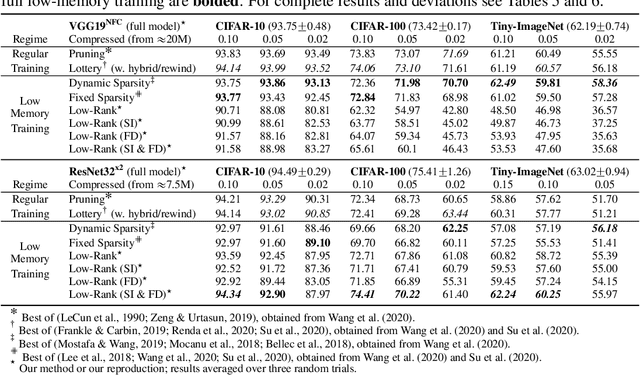
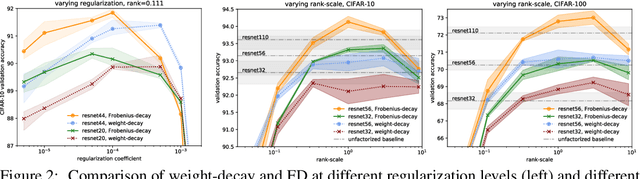
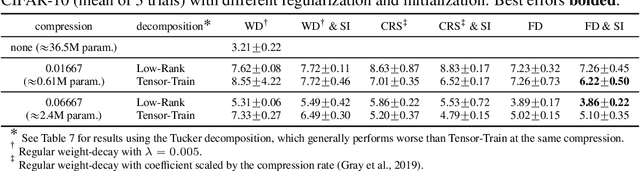
Factorized layers--operations parameterized by products of two or more matrices--occur in a variety of deep learning contexts, including compressed model training, certain types of knowledge distillation, and multi-head self-attention architectures. We study how to initialize and regularize deep nets containing such layers, examining two simple, understudied schemes, spectral initialization and Frobenius decay, for improving their performance. The guiding insight is to design optimization routines for these networks that are as close as possible to that of their well-tuned, non-decomposed counterparts; we back this intuition with an analysis of how the initialization and regularization schemes impact training with gradient descent, drawing on modern attempts to understand the interplay of weight-decay and batch-normalization. Empirically, we highlight the benefits of spectral initialization and Frobenius decay across a variety of settings. In model compression, we show that they enable low-rank methods to significantly outperform both unstructured sparsity and tensor methods on the task of training low-memory residual networks; analogs of the schemes also improve the performance of tensor decomposition techniques. For knowledge distillation, Frobenius decay enables a simple, overcomplete baseline that yields a compact model from over-parameterized training without requiring retraining with or pruning a teacher network. Finally, we show how both schemes applied to multi-head attention lead to improved performance on both translation and unsupervised pre-training.

Gradient Flows in Dataset Space

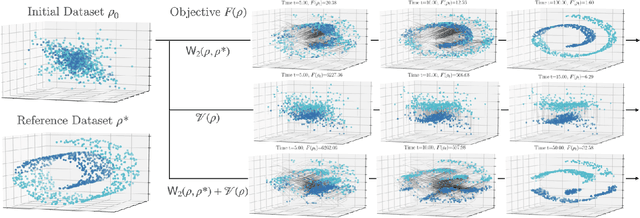
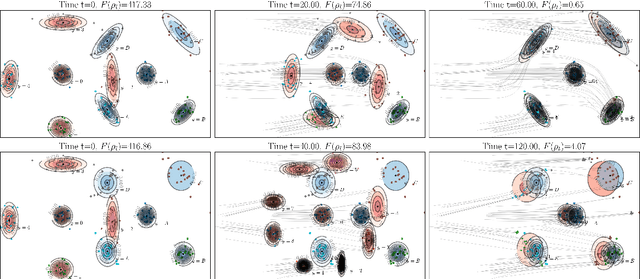
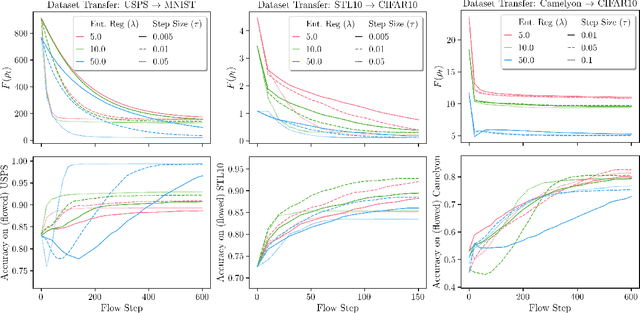
The current practice in machine learning is traditionally model-centric, casting problems as optimization over model parameters, all the while assuming the data is either fixed, or subject to extrinsic and inevitable change. On one hand, this paradigm fails to capture important existing aspects of machine learning, such as the substantial data manipulation (\emph{e.g.}, augmentation) that goes into most state-of-the-art pipelines. On the other hand, this viewpoint is ill-suited to formalize novel data-centric problems, such as model-agnostic transfer learning or dataset synthesis. In this work, we view these and other problems through the lens of \textit{dataset optimization}, casting them as optimization over data-generating distributions. We approach this class of problems through Wasserstein gradient flows in probability space, and derive practical and efficient particle-based methods for a flexible but well-behaved class of objective functions. Through various experiments on synthetic and real datasets, we show that this framework provides a principled and effective approach to dataset shaping, transfer, and interpolation.

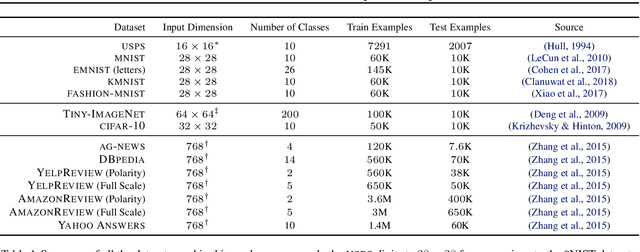
Geometric Dataset Distances via Optimal Transport

The notion of task similarity is at the core of various machine learning paradigms, such as domain adaptation and meta-learning. Current methods to quantify it are often heuristic, make strong assumptions on the label sets across the tasks, and many are architecture-dependent, relying on task-specific optimal parameters (e.g., require training a model on each dataset). In this work we propose an alternative notion of distance between datasets that (i) is model-agnostic, (ii) does not involve training, (iii) can compare datasets even if their label sets are completely disjoint and (iv) has solid theoretical footing. This distance relies on optimal transport, which provides it with rich geometry awareness, interpretable correspondences and well-understood properties. Our results show that this novel distance provides meaningful comparison of datasets, and correlates well with transfer learning hardness across various experimental settings and datasets.