Clustering-based Identification of Precursors of Extreme Events in Chaotic Systems

Abrupt and rapid high-amplitude changes in a dynamical system's states known as extreme event appear in many processes occurring in nature, such as drastic climate patterns, rogue waves, or avalanches. These events often entail catastrophic effects, therefore their description and prediction is of great importance. However, because of their chaotic nature, their modelling represents a great challenge up to this day. The applicability of a data-driven modularity-based clustering technique to identify precursors of rare and extreme events in chaotic systems is here explored. The proposed identification framework based on clustering of system states, probability transition matrices and state space tessellation was developed and tested on two different chaotic systems that exhibit extreme events: the Moehliss-Faisst-Eckhardt model of self-sustained turbulence and the 2D Kolmogorov flow. Both exhibit extreme events in the form of bursts in kinetic energy and dissipation. It is shown that the proposed framework provides a way to identify pathways towards extreme events and predict their occurrence from a probabilistic standpoint. The clustering algorithm correctly identifies the precursor states leading to extreme events and allows for a statistical description of the system's states and its precursors to extreme events.

Convolutional autoencoder for the spatiotemporal latent representation of turbulence

Turbulence is characterised by chaotic dynamics and a high-dimensional state space, which make the phenomenon challenging to predict. However, turbulent flows are often characterised by coherent spatiotemporal structures, such as vortices or large-scale modes, which can help obtain a latent description of turbulent flows. However, current approaches are often limited by either the need to use some form of thresholding on quantities defining the isosurfaces to which the flow structures are associated or the linearity of traditional modal flow decomposition approaches, such as those based on proper orthogonal decomposition. This problem is exacerbated in flows that exhibit extreme events, which are rare and sudden changes in a turbulent state. The goal of this paper is to obtain an efficient and accurate reduced-order latent representation of a turbulent flow that exhibits extreme events. Specifically, we employ a three-dimensional multiscale convolutional autoencoder (CAE) to obtain such latent representation. We apply it to a three-dimensional turbulent flow. We show that the Multiscale CAE is efficient, requiring less than 10% degrees of freedom than proper orthogonal decomposition for compressing the data and is able to accurately reconstruct flow states related to extreme events. The proposed deep learning architecture opens opportunities for nonlinear reduced-order modeling of turbulent flows from data.

Modelling spatiotemporal turbulent dynamics with the convolutional autoencoder echo state network

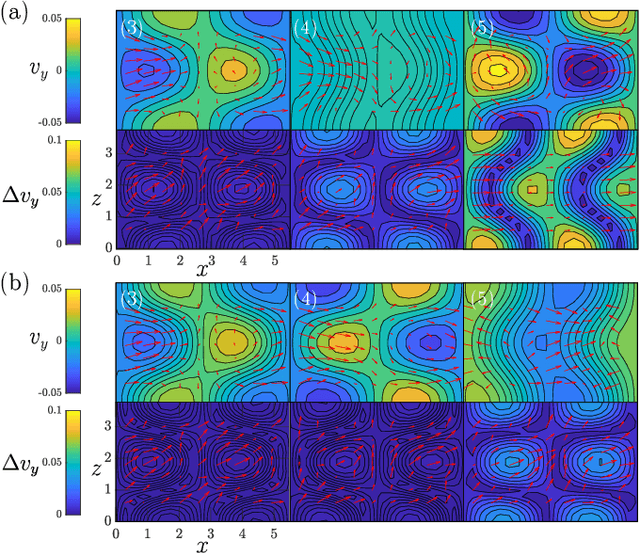
The spatiotemporal dynamics of turbulent flows is chaotic and difficult to predict. This makes the design of accurate and stable reduced-order models challenging. The overarching objective of this paper is to propose a nonlinear decomposition of the turbulent state for a reduced-order representation of the dynamics. We divide the turbulent flow into a spatial problem and a temporal problem. First, we compute the latent space, which is the manifold onto which the turbulent dynamics live (i.e., it is a numerical approximation of the turbulent attractor). The latent space is found by a series of nonlinear filtering operations, which are performed by a convolutional autoencoder (CAE). The CAE provides the decomposition in space. Second, we predict the time evolution of the turbulent state in the latent space, which is performed by an echo state network (ESN). The ESN provides the decomposition in time. Third, by assembling the CAE and the ESN, we obtain an autonomous dynamical system: the convolutional autoncoder echo state network (CAE-ESN). This is the reduced-order model of the turbulent flow. We test the CAE-ESN on a two-dimensional flow. We show that, after training, the CAE-ESN (i) finds a latent-space representation of the turbulent flow that has less than 1% of the degrees of freedom than the physical space; (ii) time-accurately and statistically predicts the flow in both quasiperiodic and turbulent regimes; (iii) is robust for different flow regimes (Reynolds numbers); and (iv) takes less than 1% of computational time to predict the turbulent flow than solving the governing equations. This work opens up new possibilities for nonlinear decompositions and reduced-order modelling of turbulent flows from data.

Short- and long-term prediction of a chaotic flow: A physics-constrained reservoir computing approach

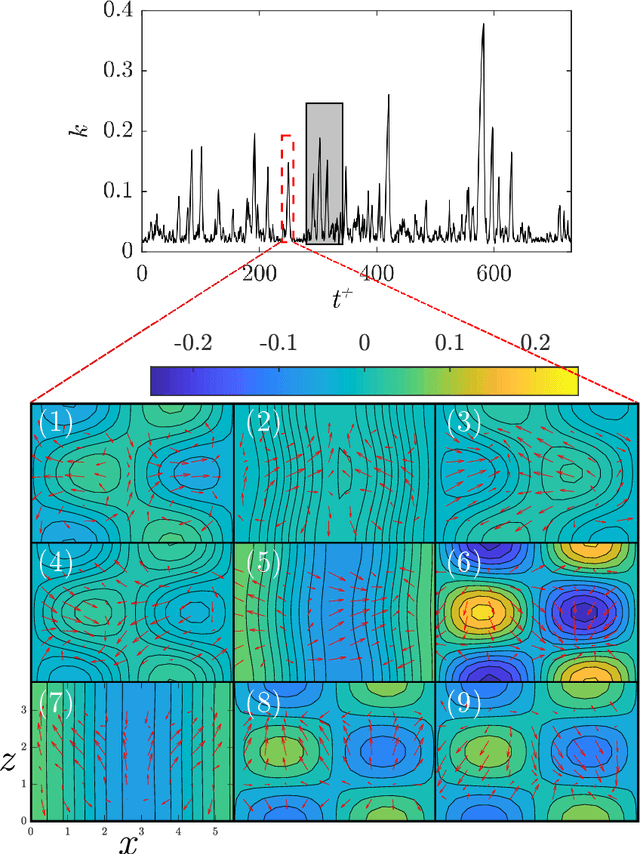
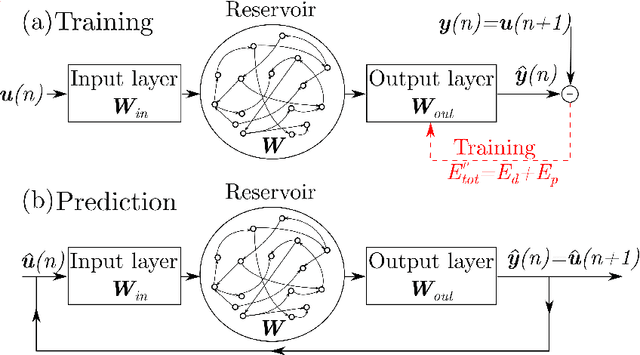
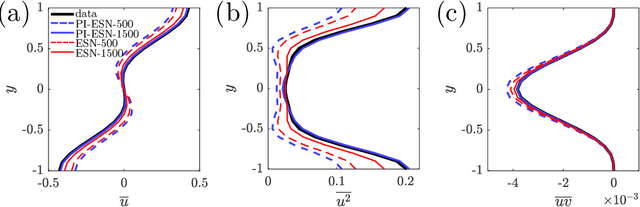
We propose a physics-constrained machine learning method-based on reservoir computing- to time-accurately predict extreme events and long-term velocity statistics in a model of turbulent shear flow. The method leverages the strengths of two different approaches: empirical modelling based on reservoir computing, which it learns the chaotic dynamics from data only, and physical modelling based on conservation laws, which extrapolates the dynamics when training data becomes unavailable. We show that the combination of the two approaches is able to accurately reproduce the velocity statistics and to predict the occurrence and amplitude of extreme events in a model of self-sustaining process in turbulence. In this flow, the extreme events are abrupt transitions from turbulent to quasi-laminar states, which are deterministic phenomena that cannot be traditionally predicted because of chaos. Furthermore, the physics-constrained machine learning method is shown to be robust with respect to noise. This work opens up new possibilities for synergistically enhancing data-driven methods with physical knowledge for the time-accurate prediction of chaotic flows.

Auto-Encoded Reservoir Computing for Turbulence Learning

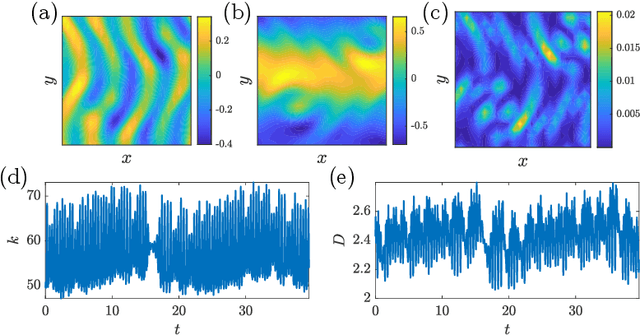
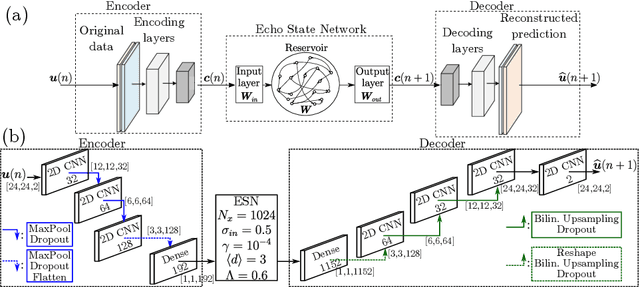
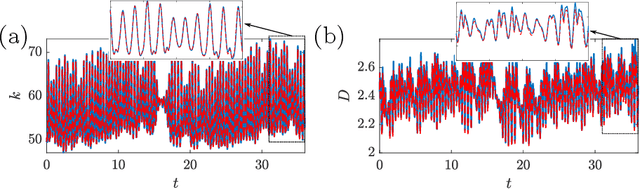
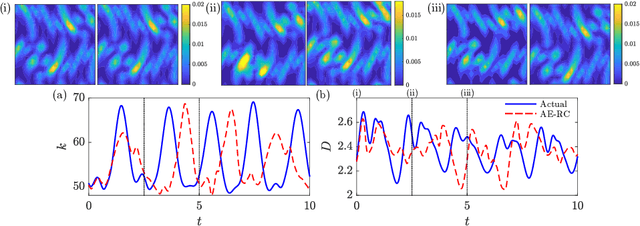
We present an Auto-Encoded Reservoir-Computing (AE-RC) approach to learn the dynamics of a 2D turbulent flow. The AE-RC consists of a Convolutional Autoencoder, which discovers an efficient manifold representation of the flow state, and an Echo State Network, which learns the time evolution of the flow in the manifold. The AE-RC is able to both learn the time-accurate dynamics of the turbulent flow and predict its first-order statistical moments. The AE-RC approach opens up new possibilities for the spatio-temporal prediction of turbulent flows with machine learning.

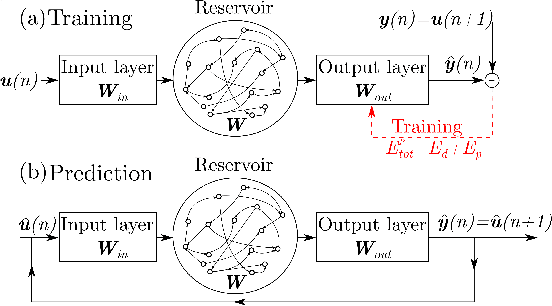
Physics-Informed Echo State Networks

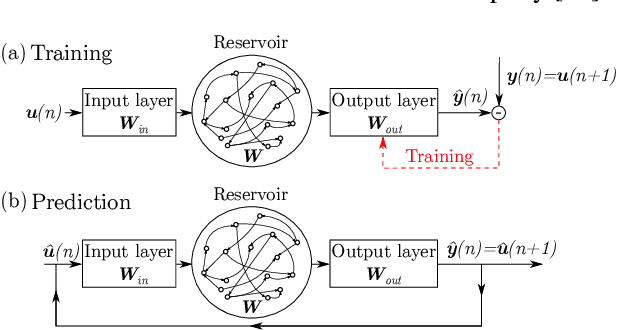
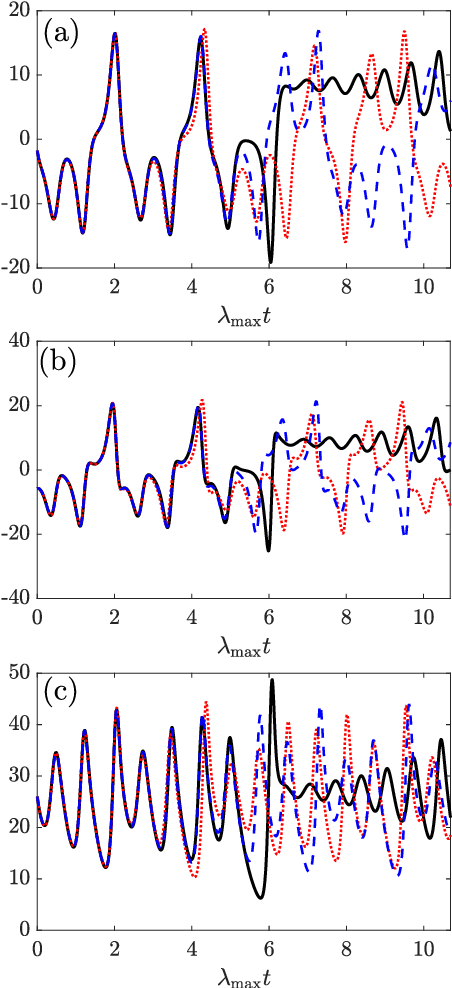
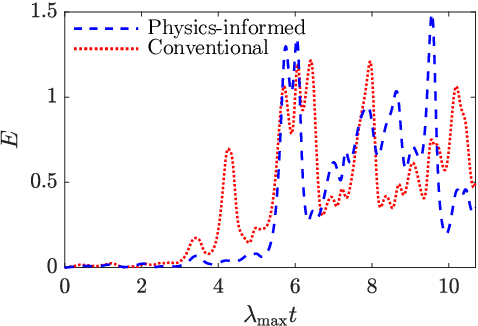
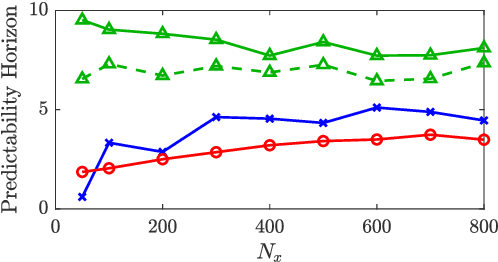
We propose a physics-informed Echo State Network (ESN) to predict the evolution of chaotic systems. Compared to conventional ESNs, the physics-informed ESNs are trained to solve supervised learning tasks while ensuring that their predictions do not violate physical laws. This is achieved by introducing an additional loss function during the training, which is based on the system's governing equations. The additional loss function penalizes non-physical predictions without the need of any additional training data. This approach is demonstrated on a chaotic Lorenz system and a truncation of the Charney-DeVore system. Compared to the conventional ESNs, the physics-informed ESNs improve the predictability horizon by about two Lyapunov times. This approach is also shown to be robust with regard to noise. The proposed framework shows the potential of using machine learning combined with prior physical knowledge to improve the time-accurate prediction of chaotic dynamical systems.

Learning Hidden States in a Chaotic System: A Physics-Informed Echo State Network Approach

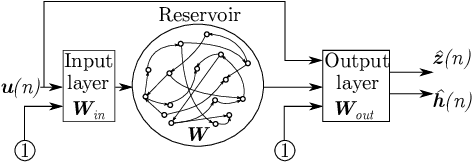
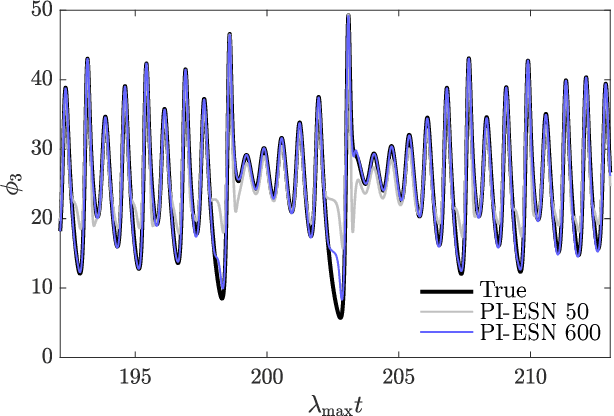
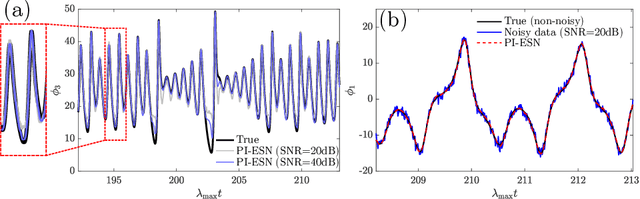
We extend the Physics-Informed Echo State Network (PI-ESN) framework to reconstruct the evolution of an unmeasured state (hidden state) in a chaotic system. The PI-ESN is trained by using (i) data, which contains no information on the unmeasured state, and (ii) the physical equations of a prototypical chaotic dynamical system. Non-noisy and noisy datasets are considered. First, it is shown that the PI-ESN can accurately reconstruct the unmeasured state. Second, the reconstruction is shown to be robust with respect to noisy data, which means that the PI-ESN acts as a denoiser. This paper opens up new possibilities for leveraging the synergy between physical knowledge and machine learning to enhance the reconstruction and prediction of unmeasured states in chaotic dynamical systems.

A physics-aware machine to predict extreme events in turbulence

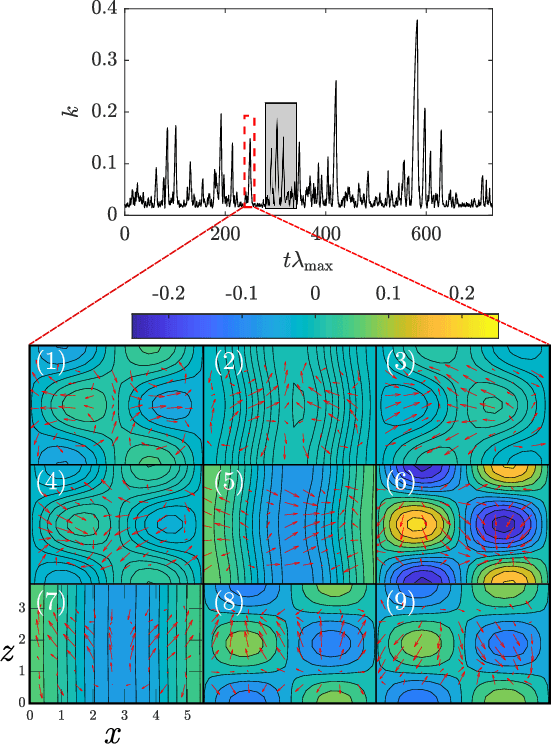
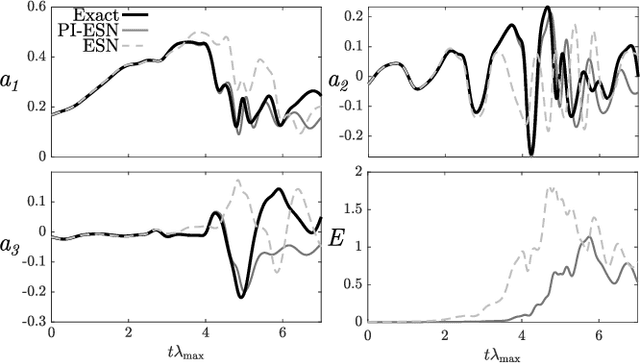
We propose a physics-aware machine learning method to time-accurately predict extreme events in a turbulent flow. The method combines two radically different approaches: empirical modelling based on reservoir computing, which learns the chaotic dynamics from data only, and physical modelling based on conservation laws. We show that the combination of the two approaches is able to predict the occurrence and amplitude of extreme events in the self-sustaining process in turbulence-the abrupt transitions from turbulent to quasi-laminar states-which cannot be achieved by using either approach separately. This opens up new possibilities for enhancing synergistically data-driven methods with physical knowledge for the accurate prediction of extreme events in chaotic dynamical systems.