Short- and long-term prediction of a chaotic flow: A physics-constrained reservoir computing approach

We propose a physics-constrained machine learning method-based on reservoir computing- to time-accurately predict extreme events and long-term velocity statistics in a model of turbulent shear flow. The method leverages the strengths of two different approaches: empirical modelling based on reservoir computing, which it learns the chaotic dynamics from data only, and physical modelling based on conservation laws, which extrapolates the dynamics when training data becomes unavailable. We show that the combination of the two approaches is able to accurately reproduce the velocity statistics and to predict the occurrence and amplitude of extreme events in a model of self-sustaining process in turbulence. In this flow, the extreme events are abrupt transitions from turbulent to quasi-laminar states, which are deterministic phenomena that cannot be traditionally predicted because of chaos. Furthermore, the physics-constrained machine learning method is shown to be robust with respect to noise. This work opens up new possibilities for synergistically enhancing data-driven methods with physical knowledge for the time-accurate prediction of chaotic flows.

Auto-Encoded Reservoir Computing for Turbulence Learning

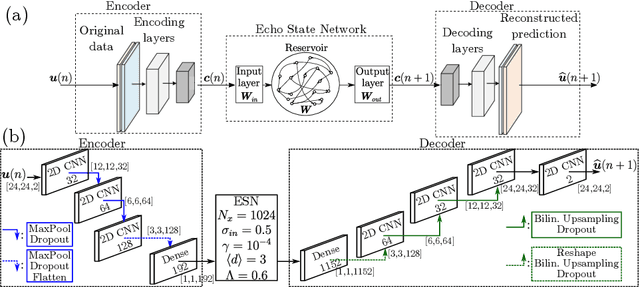
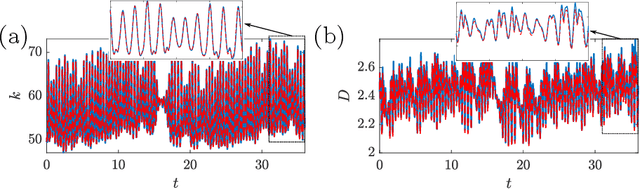
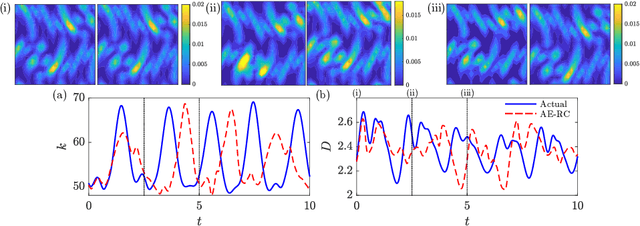
We present an Auto-Encoded Reservoir-Computing (AE-RC) approach to learn the dynamics of a 2D turbulent flow. The AE-RC consists of a Convolutional Autoencoder, which discovers an efficient manifold representation of the flow state, and an Echo State Network, which learns the time evolution of the flow in the manifold. The AE-RC is able to both learn the time-accurate dynamics of the turbulent flow and predict its first-order statistical moments. The AE-RC approach opens up new possibilities for the spatio-temporal prediction of turbulent flows with machine learning.

Physics-Informed Echo State Networks

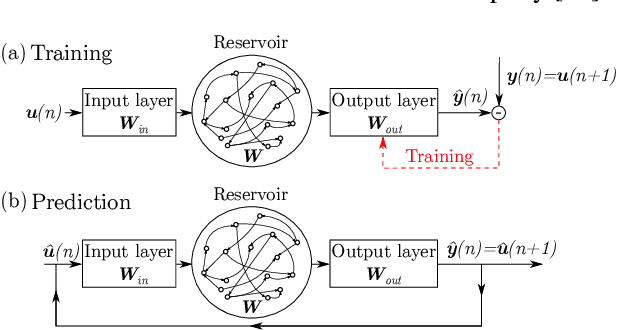
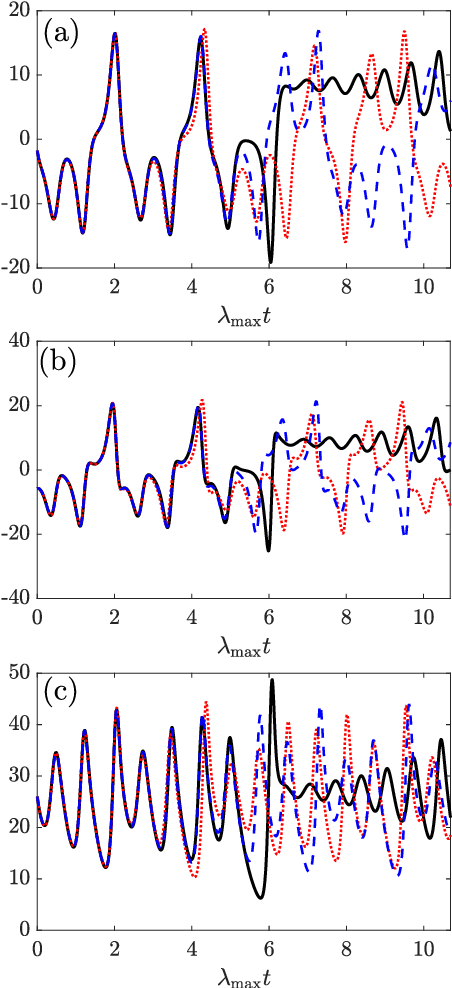
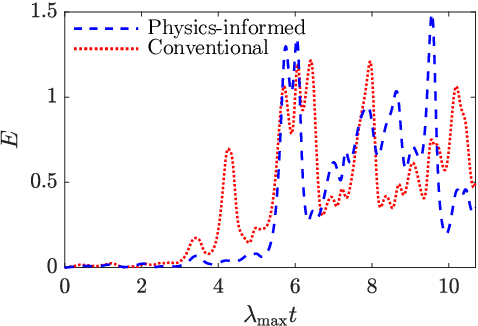
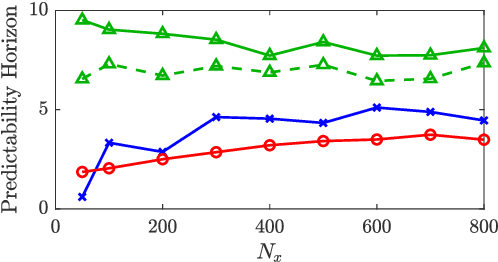
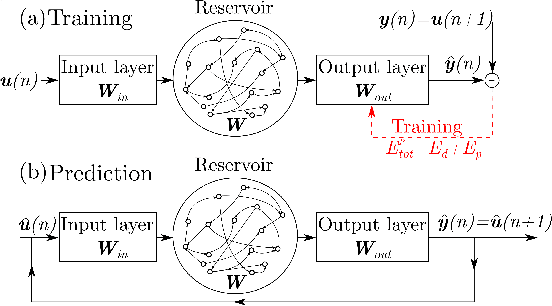
We propose a physics-informed Echo State Network (ESN) to predict the evolution of chaotic systems. Compared to conventional ESNs, the physics-informed ESNs are trained to solve supervised learning tasks while ensuring that their predictions do not violate physical laws. This is achieved by introducing an additional loss function during the training, which is based on the system's governing equations. The additional loss function penalizes non-physical predictions without the need of any additional training data. This approach is demonstrated on a chaotic Lorenz system and a truncation of the Charney-DeVore system. Compared to the conventional ESNs, the physics-informed ESNs improve the predictability horizon by about two Lyapunov times. This approach is also shown to be robust with regard to noise. The proposed framework shows the potential of using machine learning combined with prior physical knowledge to improve the time-accurate prediction of chaotic dynamical systems.

Learning Hidden States in a Chaotic System: A Physics-Informed Echo State Network Approach

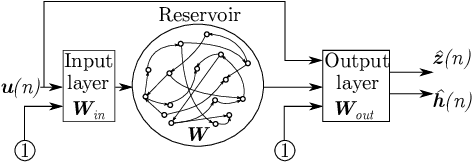
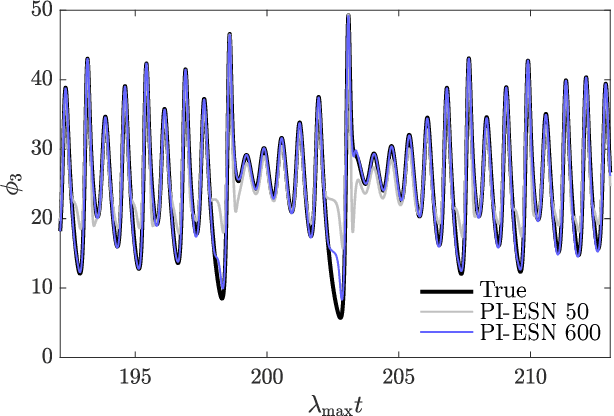
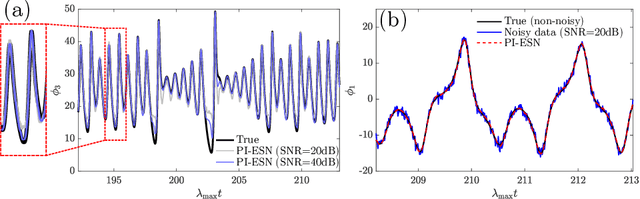
We extend the Physics-Informed Echo State Network (PI-ESN) framework to reconstruct the evolution of an unmeasured state (hidden state) in a chaotic system. The PI-ESN is trained by using (i) data, which contains no information on the unmeasured state, and (ii) the physical equations of a prototypical chaotic dynamical system. Non-noisy and noisy datasets are considered. First, it is shown that the PI-ESN can accurately reconstruct the unmeasured state. Second, the reconstruction is shown to be robust with respect to noisy data, which means that the PI-ESN acts as a denoiser. This paper opens up new possibilities for leveraging the synergy between physical knowledge and machine learning to enhance the reconstruction and prediction of unmeasured states in chaotic dynamical systems.

A physics-aware machine to predict extreme events in turbulence

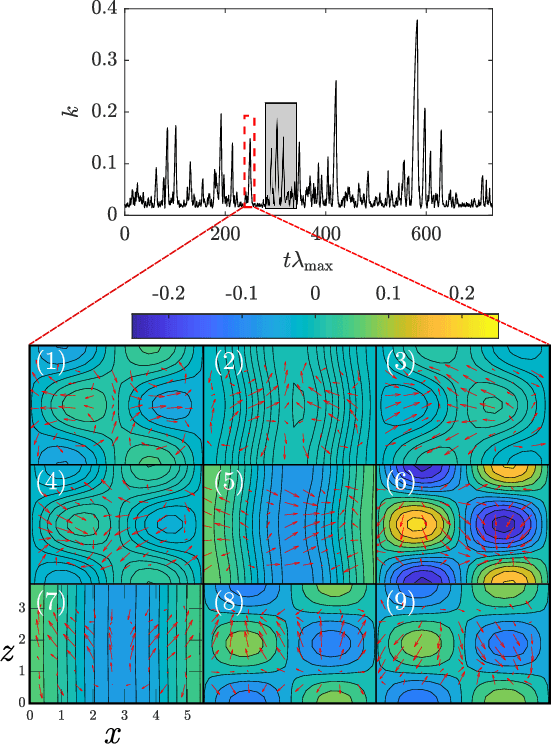
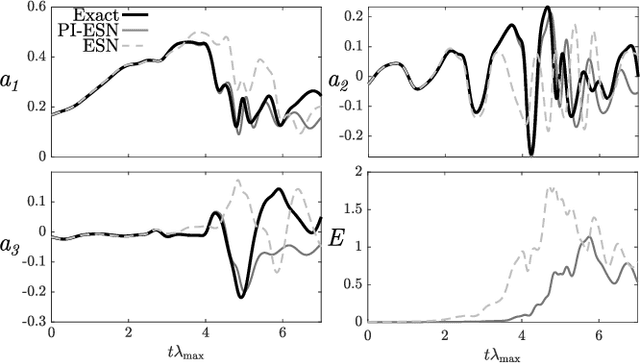
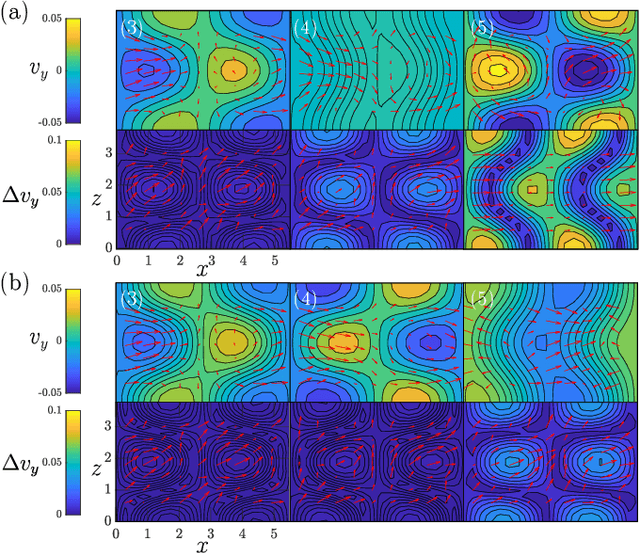
We propose a physics-aware machine learning method to time-accurately predict extreme events in a turbulent flow. The method combines two radically different approaches: empirical modelling based on reservoir computing, which learns the chaotic dynamics from data only, and physical modelling based on conservation laws. We show that the combination of the two approaches is able to predict the occurrence and amplitude of extreme events in the self-sustaining process in turbulence-the abrupt transitions from turbulent to quasi-laminar states-which cannot be achieved by using either approach separately. This opens up new possibilities for enhancing synergistically data-driven methods with physical knowledge for the accurate prediction of extreme events in chaotic dynamical systems.