Control-aware echo state networks for the suppression of extreme events

Extreme event are sudden large-amplitude changes in the state or observables of chaotic nonlinear systems, which characterize many scientific phenomena. Because of their violent nature, extreme events typically have adverse consequences, which call for methods to prevent the events from happening. In this work, we introduce the control-aware echo state network (Ca-ESN) to seamlessly combine ESNs and control strategies, such as proportional-integral-derivative and model predictive control, to suppress extreme events. The methodology is showcased on a chaotic-turbulent flow, in which we reduce the occurrence of extreme events with respect to traditional methods by two orders of magnitude. This works opens up new possibilities for the efficient control of nonlinear systems with neural networks.

Convolutional autoencoder for the spatiotemporal latent representation of turbulence

Turbulence is characterised by chaotic dynamics and a high-dimensional state space, which make the phenomenon challenging to predict. However, turbulent flows are often characterised by coherent spatiotemporal structures, such as vortices or large-scale modes, which can help obtain a latent description of turbulent flows. However, current approaches are often limited by either the need to use some form of thresholding on quantities defining the isosurfaces to which the flow structures are associated or the linearity of traditional modal flow decomposition approaches, such as those based on proper orthogonal decomposition. This problem is exacerbated in flows that exhibit extreme events, which are rare and sudden changes in a turbulent state. The goal of this paper is to obtain an efficient and accurate reduced-order latent representation of a turbulent flow that exhibits extreme events. Specifically, we employ a three-dimensional multiscale convolutional autoencoder (CAE) to obtain such latent representation. We apply it to a three-dimensional turbulent flow. We show that the Multiscale CAE is efficient, requiring less than 10% degrees of freedom than proper orthogonal decomposition for compressing the data and is able to accurately reconstruct flow states related to extreme events. The proposed deep learning architecture opens opportunities for nonlinear reduced-order modeling of turbulent flows from data.

Modelling spatiotemporal turbulent dynamics with the convolutional autoencoder echo state network

The spatiotemporal dynamics of turbulent flows is chaotic and difficult to predict. This makes the design of accurate and stable reduced-order models challenging. The overarching objective of this paper is to propose a nonlinear decomposition of the turbulent state for a reduced-order representation of the dynamics. We divide the turbulent flow into a spatial problem and a temporal problem. First, we compute the latent space, which is the manifold onto which the turbulent dynamics live (i.e., it is a numerical approximation of the turbulent attractor). The latent space is found by a series of nonlinear filtering operations, which are performed by a convolutional autoencoder (CAE). The CAE provides the decomposition in space. Second, we predict the time evolution of the turbulent state in the latent space, which is performed by an echo state network (ESN). The ESN provides the decomposition in time. Third, by assembling the CAE and the ESN, we obtain an autonomous dynamical system: the convolutional autoncoder echo state network (CAE-ESN). This is the reduced-order model of the turbulent flow. We test the CAE-ESN on a two-dimensional flow. We show that, after training, the CAE-ESN (i) finds a latent-space representation of the turbulent flow that has less than 1% of the degrees of freedom than the physical space; (ii) time-accurately and statistically predicts the flow in both quasiperiodic and turbulent regimes; (iii) is robust for different flow regimes (Reynolds numbers); and (iv) takes less than 1% of computational time to predict the turbulent flow than solving the governing equations. This work opens up new possibilities for nonlinear decompositions and reduced-order modelling of turbulent flows from data.

Data-driven prediction and control of extreme events in a chaotic flow

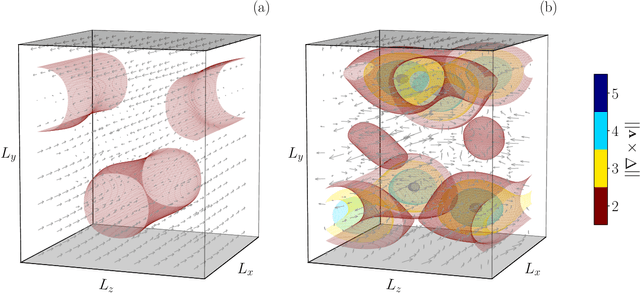
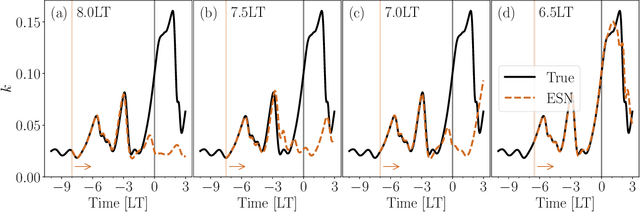
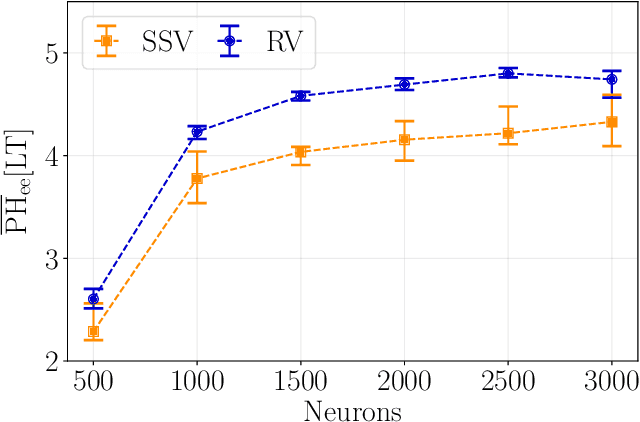
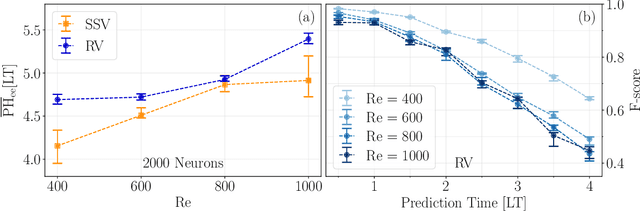
An extreme event is a sudden and violent change in the state of a nonlinear system. In fluid dynamics, extreme events can have adverse effects on the system's optimal design and operability, which calls for accurate methods for their prediction and control. In this paper, we propose a data-driven methodology for the prediction and control of extreme events in a chaotic shear flow. The approach is based on echo state networks, which are a type of reservoir computing that learn temporal correlations within a time-dependent dataset. The objective is five-fold. First, we exploit ad-hoc metrics from binary classification to analyse (i) how many of the extreme events predicted by the network actually occur in the test set (precision), and (ii) how many extreme events are missed by the network (recall). We apply a principled strategy for optimal hyperparameter selection, which is key to the networks' performance. Second, we focus on the time-accurate prediction of extreme events. We show that echo state networks are able to predict extreme events well beyond the predictability time, i.e., up to more than five Lyapunov times. Third, we focus on the long-term prediction of extreme events from a statistical point of view. By training the networks with datasets that contain non-converged statistics, we show that the networks are able to learn and extrapolate the flow's long-term statistics. In other words, the networks are able to extrapolate in time from relatively short time series. Fourth, we design a simple and effective control strategy to prevent extreme events from occurring. The control strategy decreases the occurrence of extreme events up to one order of magnitude with respect to the uncontrolled system. Finally, we analyse the robustness of the results for a range of Reynolds numbers. We show that the networks perform well across a wide range of regimes.

Statistical prediction of extreme events from small datasets

We propose Echo State Networks (ESNs) to predict the statistics of extreme events in a turbulent flow. We train the ESNs on small datasets that lack information about the extreme events. We asses whether the networks are able to extrapolate from the small imperfect datasets and predict the heavy-tail statistics that describe the events. We find that the networks correctly predict the events and improve the statistics of the system with respect to the training data in almost all cases analysed. This opens up new possibilities for the statistical prediction of extreme events in turbulence.

Robust Optimization and Validation of Echo State Networks for learning chaotic dynamics

An approach to the time-accurate prediction of chaotic solutions is by learning temporal patterns from data. Echo State Networks (ESNs), which are a class of Reservoir Computing, can accurately predict the chaotic dynamics well beyond the predictability time. Existing studies, however, also showed that small changes in the hyperparameters may markedly affect the network's performance. The aim of this paper is to assess and improve the robustness of Echo State Networks for the time-accurate prediction of chaotic solutions. The goal is three-fold. First, we investigate the robustness of routinely used validation strategies. Second, we propose the Recycle Validation, and the chaotic versions of existing validation strategies, to specifically tackle the forecasting of chaotic systems. Third, we compare Bayesian optimization with the traditional Grid Search for optimal hyperparameter selection. Numerical tests are performed on two prototypical nonlinear systems that have both chaotic and quasiperiodic solutions. Both model-free and model-informed Echo State Networks are analysed. By comparing the network's robustness in learning chaotic versus quasiperiodic solutions, we highlight fundamental challenges in learning chaotic solutions. The proposed validation strategies, which are based on the dynamical systems properties of chaotic time series, are shown to outperform the state-of-the-art validation strategies. Because the strategies are principled-they are based on chaos theory such as the Lyapunov time-they can be applied to other Recurrent Neural Networks architectures with little modification. This work opens up new possibilities for the robust design and application of Echo State Networks, and Recurrent Neural Networks, to the time-accurate prediction of chaotic systems.

Automatic-differentiated Physics-Informed Echo State Network (API-ESN)

We propose the Automatic-differentiated Physics-Informed Echo State Network (API-ESN). The architecture constrains the knowledge of the physical equations through the reservoir's exact time derivative, which is computed by automatic differentiation. As compared to the original Physics-Informed Echo State Network, the accuracy of the time derivative is increased by up to seven orders of magnitude. This increased accuracy is key in chaotic dynamical systems, where errors grows exponentially in time. The architecture is showcased in the reconstruction of unmeasured (hidden) states of a chaotic system. The API-ESN eliminates a source of error, which is present in existing physics-informed echo state networks, in the computation of the time-derivative. This opens up new possibilities for an accurate reconstruction of chaotic dynamical states.