Efficient Local Planning with Linear Function Approximation

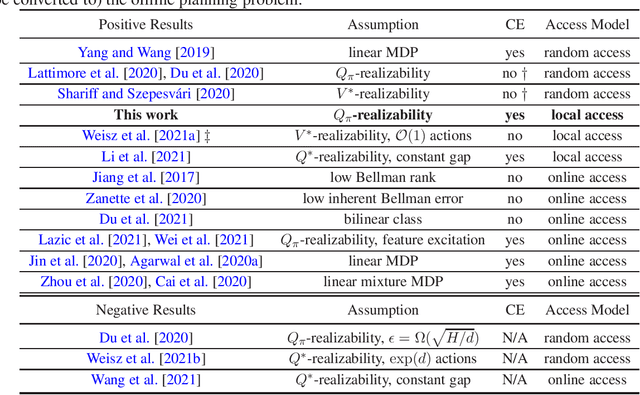
We study query and computationally efficient planning algorithms with linear function approximation and a simulator. We assume that the agent only has local access to the simulator, meaning that the agent can only query the simulator at states that have been visited before. This setting is more practical than many prior works on reinforcement learning with a generative model. We propose an algorithm named confident Monte Carlo least square policy iteration (Confident MC-LSPI) for this setting. Under the assumption that the Q-functions of all deterministic policies are linear in known features of the state-action pairs, we show that our algorithm has polynomial query and computational complexities in the dimension of the features, the effective planning horizon and the targeted sub-optimality, while these complexities are independent of the size of the state space. One technical contribution of our work is the introduction of a novel proof technique that makes use of a virtual policy iteration algorithm. We use this method to leverage existing results on $\ell_\infty$-bounded approximate policy iteration to show that our algorithm can learn the optimal policy for the given initial state even only with local access to the simulator. We believe that this technique can be extended to broader settings beyond this work.

Optimization Issues in KL-Constrained Approximate Policy Iteration

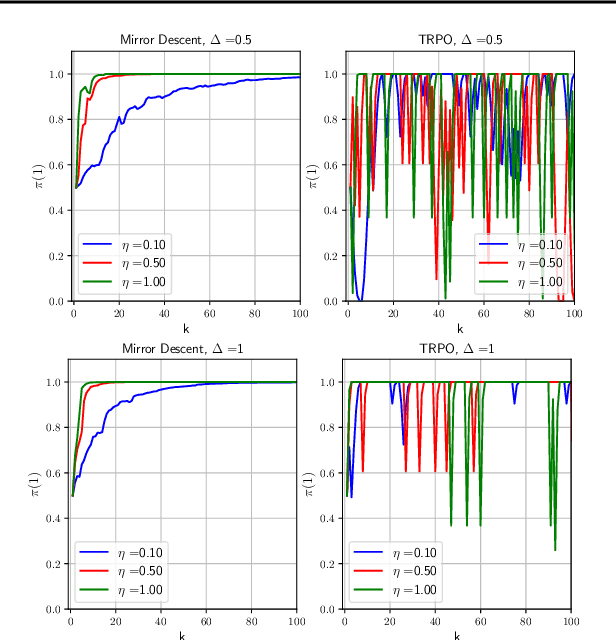
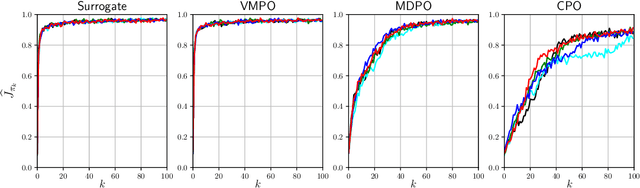
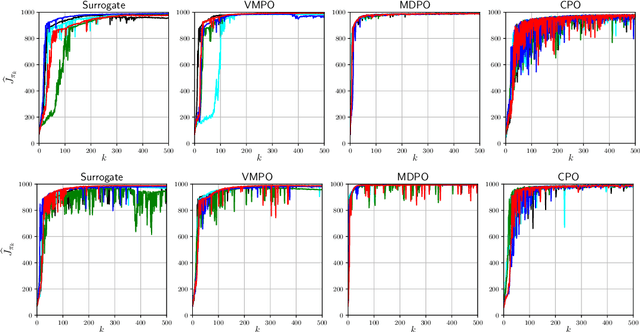
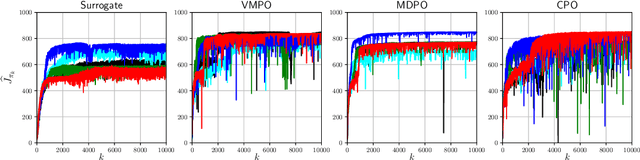
Many reinforcement learning algorithms can be seen as versions of approximate policy iteration (API). While standard API often performs poorly, it has been shown that learning can be stabilized by regularizing each policy update by the KL-divergence to the previous policy. Popular practical algorithms such as TRPO, MPO, and VMPO replace regularization by a constraint on KL-divergence of consecutive policies, arguing that this is easier to implement and tune. In this work, we study this implementation choice in more detail. We compare the use of KL divergence as a constraint vs. as a regularizer, and point out several optimization issues with the widely-used constrained approach. We show that the constrained algorithm is not guaranteed to converge even on simple problem instances where the constrained problem can be solved exactly, and in fact incurs linear expected regret. With approximate implementation using softmax policies, we show that regularization can improve the optimization landscape of the original objective. We demonstrate these issues empirically on several bandit and RL environments.