Neil Lutz
A Center in Your Neighborhood: Fairness in Facility Location
Aug 30, 2019
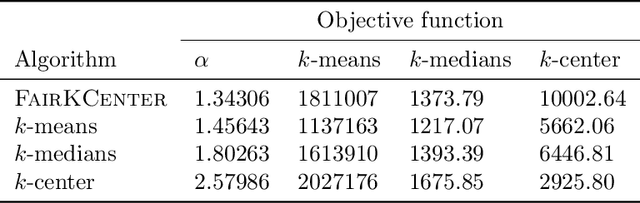
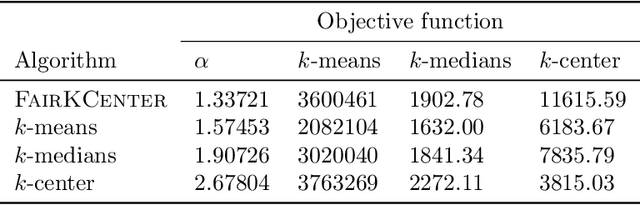
Abstract:When selecting locations for a set of facilities, standard clustering algorithms may place unfair burden on some individuals and neighborhoods. We formulate a fairness concept that takes local population densities into account. In particular, given $k$ facilities to locate and a population of size $n$, we define the "neighborhood radius" of an individual $i$ as the minimum radius of a ball centered at $i$ that contains at least $n/k$ individuals. Our objective is to ensure that each individual has a facility within at most a small constant factor of her neighborhood radius. We present several theoretical results: We show that optimizing this factor is NP-hard; we give an approximation algorithm that guarantees a factor of at most 2 in all metric spaces; and we prove matching lower bounds in some metric spaces. We apply a variant of this algorithm to real-world address data, showing that it is quite different from standard clustering algorithms and outperforms them on our objective function and balances the load between facilities more evenly.
Quantifying the Burden of Exploration and the Unfairness of Free Riding
Oct 20, 2018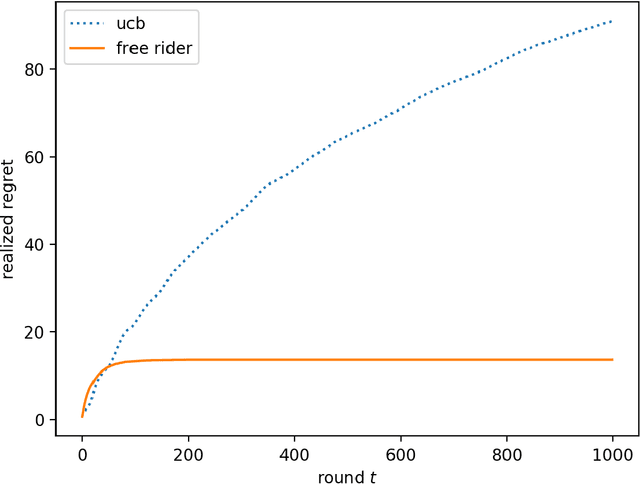
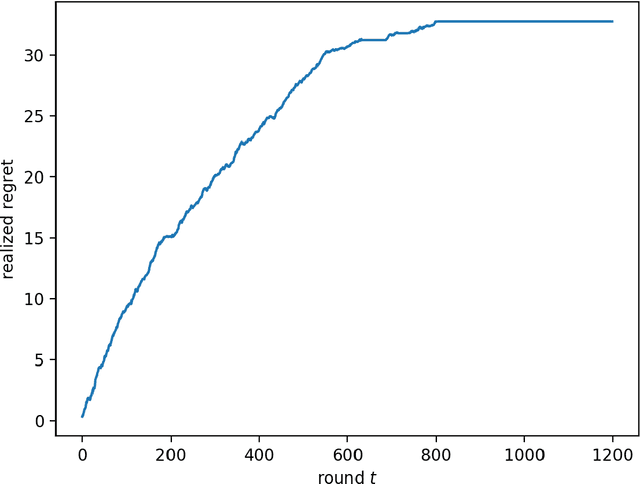
Abstract:We consider the multi-armed bandit setting with a twist. Rather than having just one decision maker deciding which arm to pull in each round, we have $n$ different decision makers (agents). In the simple stochastic setting we show that one of the agents (called the free rider), who has access to the history of other agents playing some zero regret algorithm can achieve just $O(1)$ regret, as opposed to the regret lower bound of $\Omega (\log T)$ when one decision maker is playing in isolation. In the linear contextual setting, we show that if the other agents play a particular, popular zero regret algorithm (UCB), then the free rider can again achieve $O(1)$ regret. In order to prove this result, we give a deterministic lower bound on the number of times each suboptimal arm must be pulled in UCB. In contrast, we show that the free-rider cannot beat the standard single-player regret bounds in certain partial information settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge