Navneet Agrawal
Towards Bridging the Gap between Near and Far-Field Characterizations of the Wireless Channel
Mar 10, 2024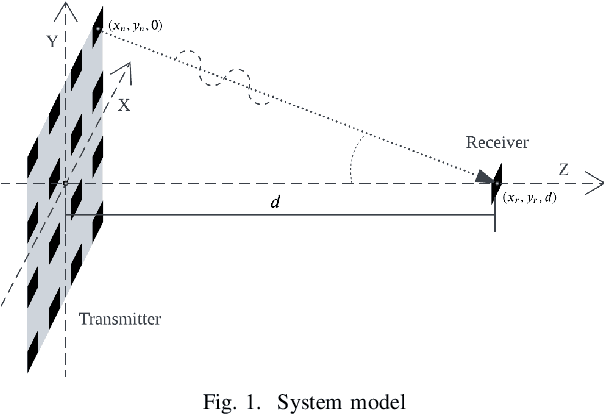
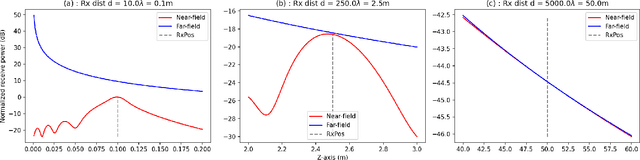
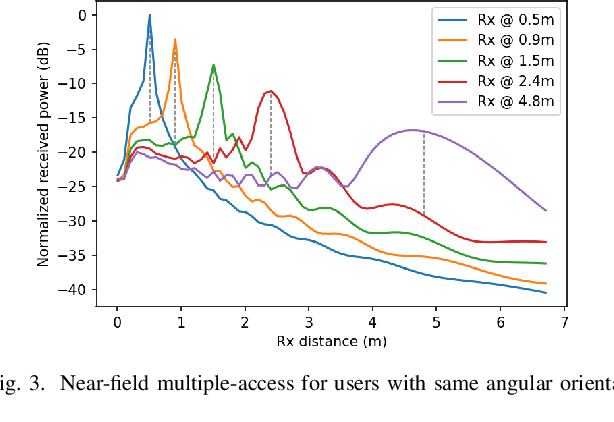
Abstract:The "near-field" propagation modeling of wireless channels is necessary to support sixth-generation (6G) technologies, such as intelligent reflecting surface (IRS), that are enabled by large aperture antennas and higher frequency carriers. As the conventional far-field model proves inadequate in this context, there is a pressing need to explore and bridge the gap between near and far-field propagation models. Although far-field models are simple and provide computationally efficient solutions for many practical applications, near-field models provide the most accurate representation of wireless channels. This paper builds upon the foundations of electromagnetic wave propagation theory to derive near and far-field models as approximations of the Green's function (Maxwell's equations). We characterize the near and far-field models both theoretically and with the help of simulations in a line-of-sight (LOS)-only scenario. In particular, for two key applications in multiantenna systems, namely, beamforming and multiple-access, we showcase the advantages of using the near-field model over the far-field, and present a novel scheduling scheme for multiple-access in the near-field regime. Our findings offer insights into the challenge of incorporating near-field models in practical wireless systems, fostering enhanced performance in future communication technologies.
A Learning-Based Approach to Approximate Coded Computation
May 19, 2022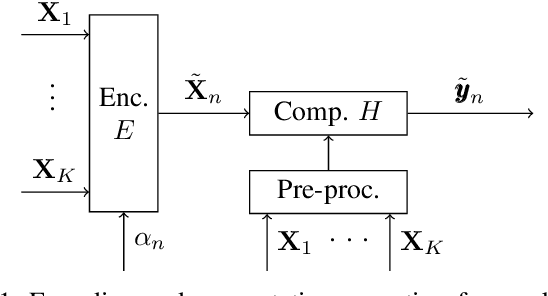
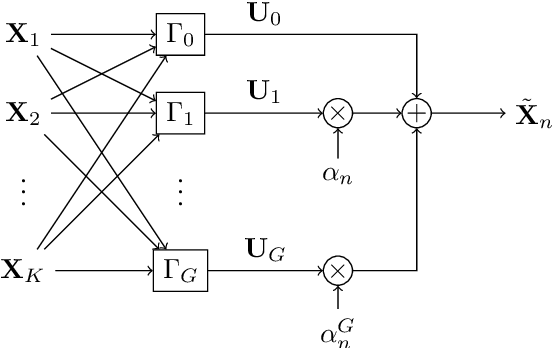
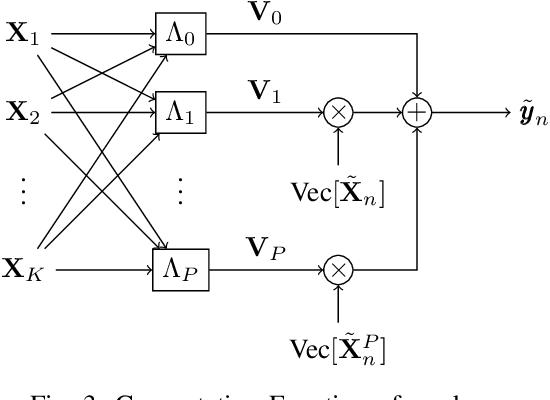
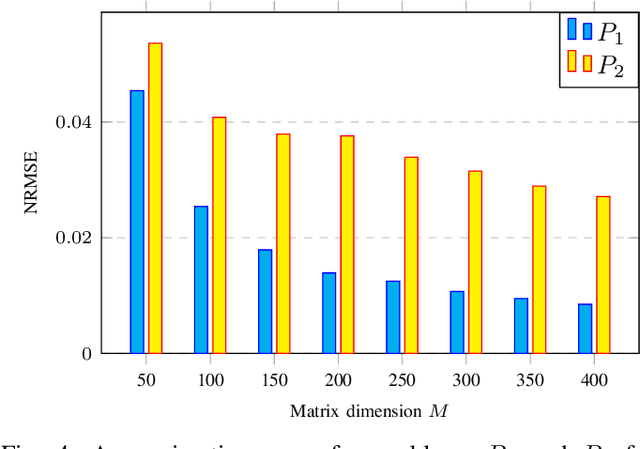
Abstract:Lagrange coded computation (LCC) is essential to solving problems about matrix polynomials in a coded distributed fashion; nevertheless, it can only solve the problems that are representable as matrix polynomials. In this paper, we propose AICC, an AI-aided learning approach that is inspired by LCC but also uses deep neural networks (DNNs). It is appropriate for coded computation of more general functions. Numerical simulations demonstrate the suitability of the proposed approach for the coded computation of different matrix functions that are often utilized in digital signal processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge