Regret Lower Bound and Optimal Algorithm for High-Dimensional Contextual Linear Bandit

In this paper, we consider the multi-armed bandit problem with high-dimensional features. First, we prove a minimax lower bound, $\mathcal{O}\big((\log d)^{\frac{\alpha+1}{2}}T^{\frac{1-\alpha}{2}}+\log T\big)$, for the cumulative regret, in terms of horizon $T$, dimension $d$ and a margin parameter $\alpha\in[0,1]$, which controls the separation between the optimal and the sub-optimal arms. This new lower bound unifies existing regret bound results that have different dependencies on T due to the use of different values of margin parameter $\alpha$ explicitly implied by their assumptions. Second, we propose a simple and computationally efficient algorithm inspired by the general Upper Confidence Bound (UCB) strategy that achieves a regret upper bound matching the lower bound. The proposed algorithm uses a properly centered $\ell_1$-ball as the confidence set in contrast to the commonly used ellipsoid confidence set. In addition, the algorithm does not require any forced sampling step and is thereby adaptive to the practically unknown margin parameter. Simulations and a real data analysis are conducted to compare the proposed method with existing ones in the literature.

Bayesian Regularization for Graphical Models with Unequal Shrinkage

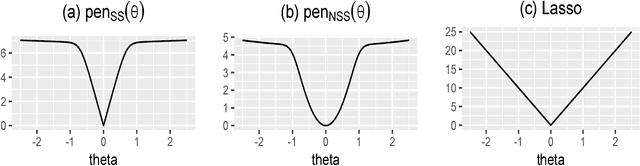
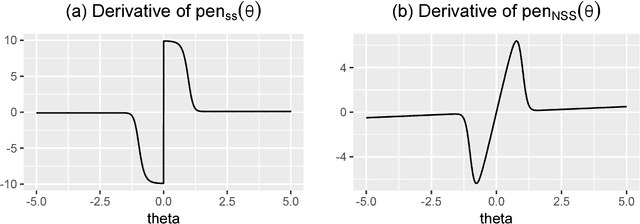
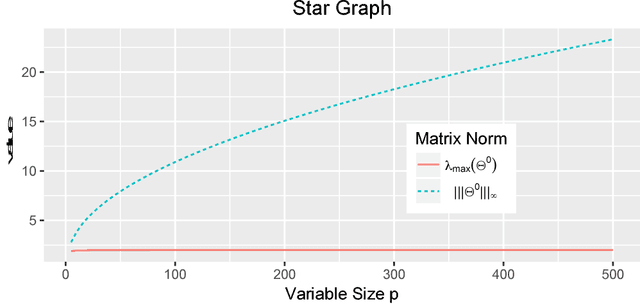
We consider a Bayesian framework for estimating a high-dimensional sparse precision matrix, in which adaptive shrinkage and sparsity are induced by a mixture of Laplace priors. Besides discussing our formulation from the Bayesian standpoint, we investigate the MAP (maximum a posteriori) estimator from a penalized likelihood perspective that gives rise to a new non-convex penalty approximating the $\ell_0$ penalty. Optimal error rates for estimation consistency in terms of various matrix norms along with selection consistency for sparse structure recovery are shown for the unique MAP estimator under mild conditions. For fast and efficient computation, an EM algorithm is proposed to compute the MAP estimator of the precision matrix and (approximate) posterior probabilities on the edges of the underlying sparse structure. Through extensive simulation studies and a real application to a call center data, we have demonstrated the fine performance of our method compared with existing alternatives.