Debugging using Orthogonal Gradient Descent

In this report we consider the following problem: Given a trained model that is partially faulty, can we correct its behaviour without having to train the model from scratch? In other words, can we ``debug" neural networks similar to how we address bugs in our mathematical models and standard computer code. We base our approach on the hypothesis that debugging can be treated as a two-task continual learning problem. In particular, we employ a modified version of a continual learning algorithm called Orthogonal Gradient Descent (OGD) to demonstrate, via two simple experiments on the MNIST dataset, that we can in-fact \textit{unlearn} the undesirable behaviour while retaining the general performance of the model, and we can additionally \textit{relearn} the appropriate behaviour, both without having to train the model from scratch.

Language Modeling using LMUs: 10x Better Data Efficiency or Improved Scaling Compared to Transformers

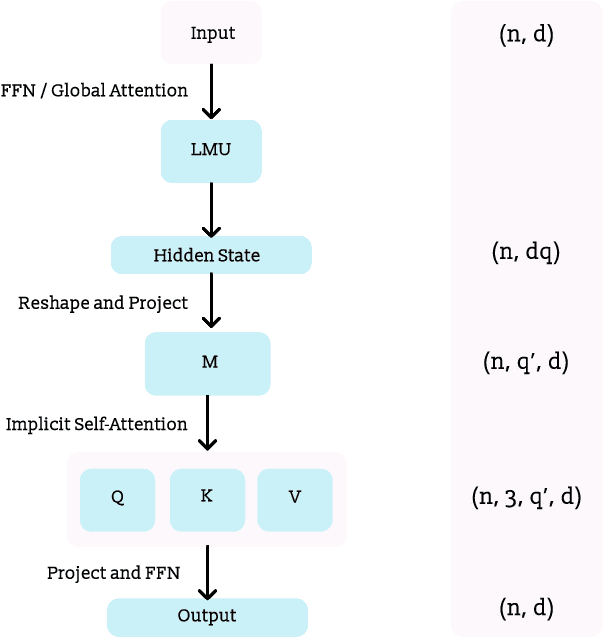
Recent studies have demonstrated that the performance of transformers on the task of language modeling obeys a power-law relationship with model size over six orders of magnitude. While transformers exhibit impressive scaling, their performance hinges on processing large amounts of data, and their computational and memory requirements grow quadratically with sequence length. Motivated by these considerations, we construct a Legendre Memory Unit based model that introduces a general prior for sequence processing and exhibits an $O(n)$ and $O(n \ln n)$ (or better) dependency for memory and computation respectively. Over three orders of magnitude, we show that our new architecture attains the same accuracy as transformers with 10x fewer tokens. We also show that for the same amount of training our model improves the loss over transformers about as much as transformers improve over LSTMs. Additionally, we demonstrate that adding global self-attention complements our architecture and the augmented model improves performance even further.

Parallelizing Legendre Memory Unit Training

Recently, a new recurrent neural network (RNN) named the Legendre Memory Unit (LMU) was proposed and shown to achieve state-of-the-art performance on several benchmark datasets. Here we leverage the linear time-invariant (LTI) memory component of the LMU to construct a simplified variant that can be parallelized during training (and yet executed as an RNN during inference), thus overcoming a well known limitation of training RNNs on GPUs. We show that this reformulation that aids parallelizing, which can be applied generally to any deep network whose recurrent components are linear, makes training up to 200 times faster. Second, to validate its utility, we compare its performance against the original LMU and a variety of published LSTM and transformer networks on seven benchmarks, ranging from psMNIST to sentiment analysis to machine translation. We demonstrate that our models exhibit superior performance on all datasets, often using fewer parameters. For instance, our LMU sets a new state-of-the-art result on psMNIST, and uses half the parameters while outperforming DistilBERT and LSTM models on IMDB sentiment analysis.