A Semiparametric Approach to Causal Inference

In causal inference, an important problem is to quantify the effects of interventions or treatments. Many studies focus on estimating the mean causal effects; however, these estimands may offer limited insight since two distributions can share the same mean yet exhibit significant differences. Examining the causal effects from a distributional perspective provides a more thorough understanding. In this paper, we employ a semiparametric density ratio model (DRM) to characterize the counterfactual distributions, introducing a framework that assumes a latent structure shared by these distributions. Our model offers flexibility by avoiding strict parametric assumptions on the counterfactual distributions. Specifically, the DRM incorporates a nonparametric component that can be estimated through the method of empirical likelihood (EL), using the data from all the groups stemming from multiple interventions. Consequently, the EL-DRM framework enables inference of the counterfactual distribution functions and their functionals, facilitating direct and transparent causal inference from a distributional perspective. Numerical studies on both synthetic and real-world data validate the effectiveness of our approach.

Statistical Inference, Learning and Models in Big Data

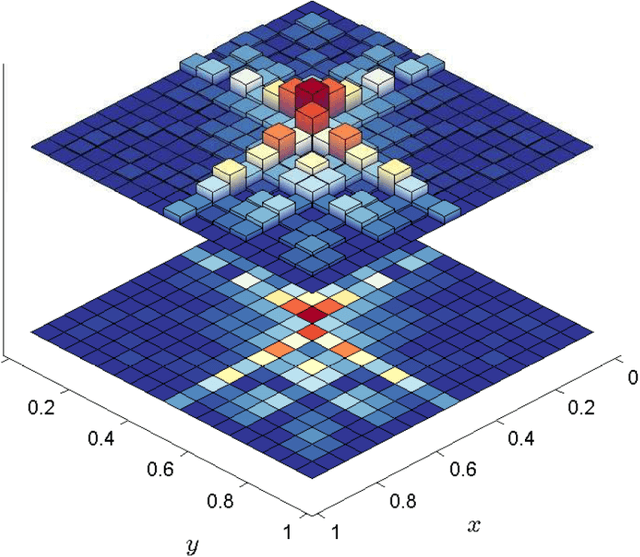
The need for new methods to deal with big data is a common theme in most scientific fields, although its definition tends to vary with the context. Statistical ideas are an essential part of this, and as a partial response, a thematic program on statistical inference, learning, and models in big data was held in 2015 in Canada, under the general direction of the Canadian Statistical Sciences Institute, with major funding from, and most activities located at, the Fields Institute for Research in Mathematical Sciences. This paper gives an overview of the topics covered, describing challenges and strategies that seem common to many different areas of application, and including some examples of applications to make these challenges and strategies more concrete.