Kernel Mean Embedding Topology: Weak and Strong Forms for Stochastic Kernels and Implications for Model Learning

We introduce a novel topology, called Kernel Mean Embedding Topology, for stochastic kernels, in a weak and strong form. This topology, defined on the spaces of Bochner integrable functions from a signal space to a space of probability measures endowed with a Hilbert space structure, allows for a versatile formulation. This construction allows one to obtain both a strong and weak formulation. (i) For its weak formulation, we highlight the utility on relaxed policy spaces, and investigate connections with the Young narrow topology and Borkar (or \( w^* \))-topology, and establish equivalence properties. We report that, while both the \( w^* \)-topology and kernel mean embedding topology are relatively compact, they are not closed. Conversely, while the Young narrow topology is closed, it lacks relative compactness. (ii) We show that the strong form provides an appropriate formulation for placing topologies on spaces of models characterized by stochastic kernels with explicit robustness and learning theoretic implications on optimal stochastic control under discounted or average cost criteria. (iii) We show that this topology possesses several properties making it ideal to study optimality, approximations, robustness and continuity properties. In particular, the kernel mean embedding topology has a Hilbert space structure, which is particularly useful for approximating stochastic kernels through simulation data.

Maximum Causal Entropy Inverse Reinforcement Learning for Mean-Field Games

In this paper, we introduce the maximum casual entropy Inverse Reinforcement Learning (IRL) problem for discrete-time mean-field games (MFGs) under an infinite-horizon discounted-reward optimality criterion. The state space of a typical agent is finite. Our approach begins with a comprehensive review of the maximum entropy IRL problem concerning deterministic and stochastic Markov decision processes (MDPs) in both finite and infinite-horizon scenarios. Subsequently, we formulate the maximum casual entropy IRL problem for MFGs - a non-convex optimization problem with respect to policies. Leveraging the linear programming formulation of MDPs, we restructure this IRL problem into a convex optimization problem and establish a gradient descent algorithm to compute the optimal solution with a rate of convergence. Finally, we present a new algorithm by formulating the MFG problem as a generalized Nash equilibrium problem (GNEP), which is capable of computing the mean-field equilibrium (MFE) for the forward RL problem. This method is employed to produce data for a numerical example. We note that this novel algorithm is also applicable to general MFE computations.

Q-Learning for MDPs with General Spaces: Convergence and Near Optimality via Quantization under Weak Continuity

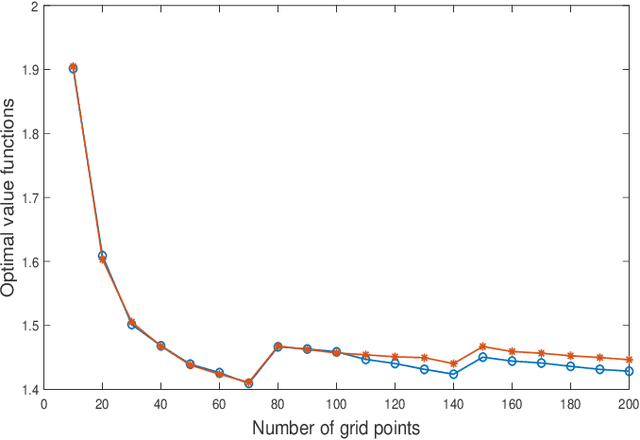
Reinforcement learning algorithms often require finiteness of state and action spaces in Markov decision processes (MDPs) and various efforts have been made in the literature towards the applicability of such algorithms for continuous state and action spaces. In this paper, we show that under very mild regularity conditions (in particular, involving only weak continuity of the transition kernel of an MDP), Q-learning for standard Borel MDPs via quantization of states and actions converge to a limit, and furthermore this limit satisfies an optimality equation which leads to near optimality with either explicit performance bounds or which are guaranteed to be asymptotically optimal. Our approach builds on (i) viewing quantization as a measurement kernel and thus a quantized MDP as a POMDP, (ii) utilizing near optimality and convergence results of Q-learning for POMDPs, and (iii) finally, near-optimality of finite state model approximations for MDPs with weakly continuous kernels which we show to correspond to the fixed point of the constructed POMDP. Thus, our paper presents a very general convergence and approximation result for the applicability of Q-learning for continuous MDPs.

Q-Learning in Regularized Mean-field Games

In this paper, we introduce a regularized mean-field game and study learning of this game under an infinite-horizon discounted reward function. The game is defined by adding a regularization function to the one-stage reward function in the classical mean-field game model. We establish a value iteration based learning algorithm to this regularized mean-field game using fitted Q-learning. This regularization term in general makes reinforcement learning algorithm more robust with improved exploration. Moreover, it enables us to establish error analysis of the learning algorithm without imposing restrictive convexity assumptions on the system components, which are needed in the absence of a regularization term.

Fitted Q-Learning in Mean-field Games

In the literature, existence of equilibria for discrete-time mean field games has been in general established via Kakutani's Fixed Point Theorem. However, this fixed point theorem does not entail any iterative scheme for computing equilibria. In this paper, we first propose a Q-iteration algorithm to compute equilibria for mean-field games with known model using Banach Fixed Point Theorem. Then, we generalize this algorithm to model-free setting using fitted Q-iteration algorithm and establish the probabilistic convergence of the proposed iteration. Then, using the output of this learning algorithm, we construct an approximate Nash equilibrium for finite-agent stochastic game with mean-field interaction between agents.