Naama Haramaty-Krasne
Low Rank Field-Weighted Factorization Machines for Low Latency Item Recommendation
Jul 22, 2024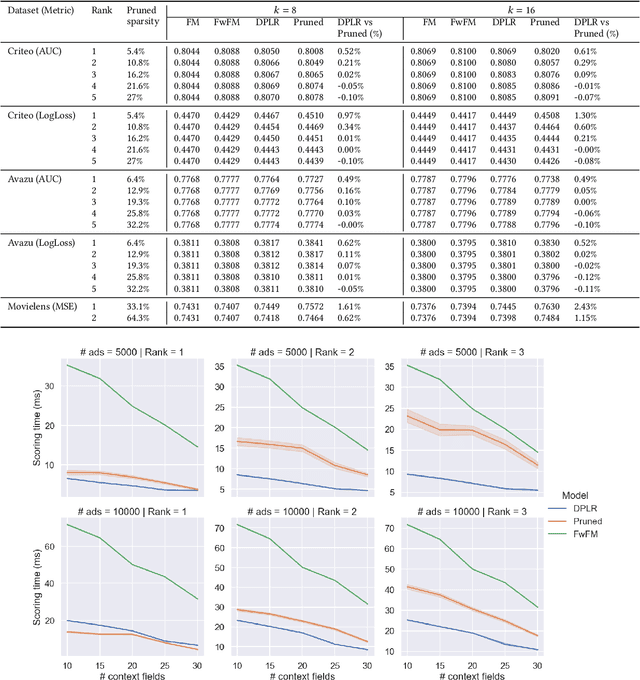
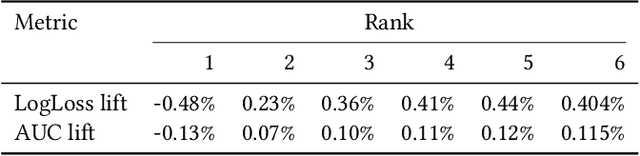
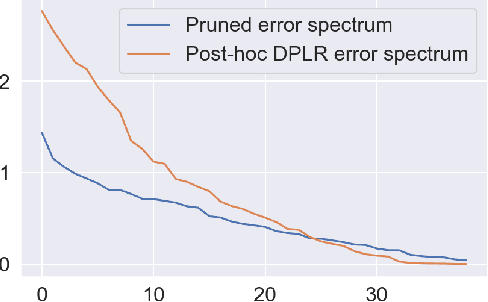

Abstract:Factorization machine (FM) variants are widely used in recommendation systems that operate under strict throughput and latency requirements, such as online advertising systems. FMs are known both due to their ability to model pairwise feature interactions while being resilient to data sparsity, and their computational graphs that facilitate fast inference and training. Moreover, when items are ranked as a part of a query for each incoming user, these graphs facilitate computing the portion stemming from the user and context fields only once per query. Consequently, in terms of inference cost, the number of user or context fields is practically unlimited. More advanced FM variants, such as FwFM, provide better accuracy by learning a representation of field-wise interactions, but require computing all pairwise interaction terms explicitly. The computational cost during inference is proportional to the square of the number of fields, including user, context, and item. When the number of fields is large, this is prohibitive in systems with strict latency constraints. To mitigate this caveat, heuristic pruning of low intensity field interactions is commonly used to accelerate inference. In this work we propose an alternative to the pruning heuristic in FwFMs using a diagonal plus symmetric low-rank decomposition. Our technique reduces the computational cost of inference, by allowing it to be proportional to the number of item fields only. Using a set of experiments on real-world datasets, we show that aggressive rank reduction outperforms similarly aggressive pruning, both in terms of accuracy and item recommendation speed. We corroborate our claim of faster inference experimentally, both via a synthetic test, and by having deployed our solution to a major online advertising system. The code to reproduce our experimental results is at https://github.com/michaelviderman/pytorch-fm/tree/dev.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge