Finding Numerical Solutions of Diophantine Equations using Ant Colony Optimization

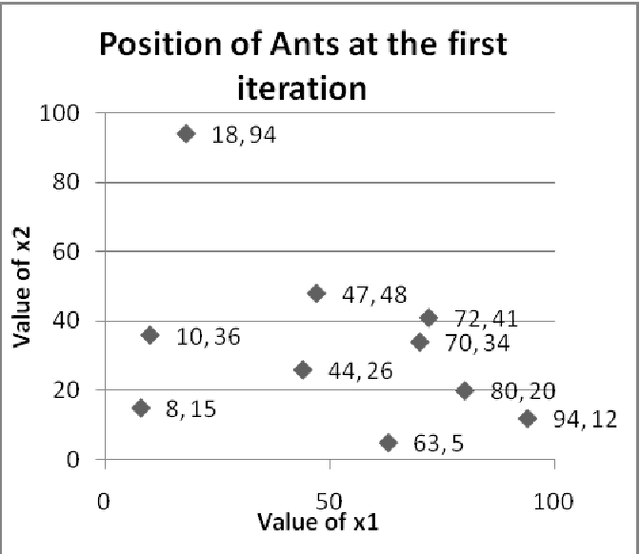
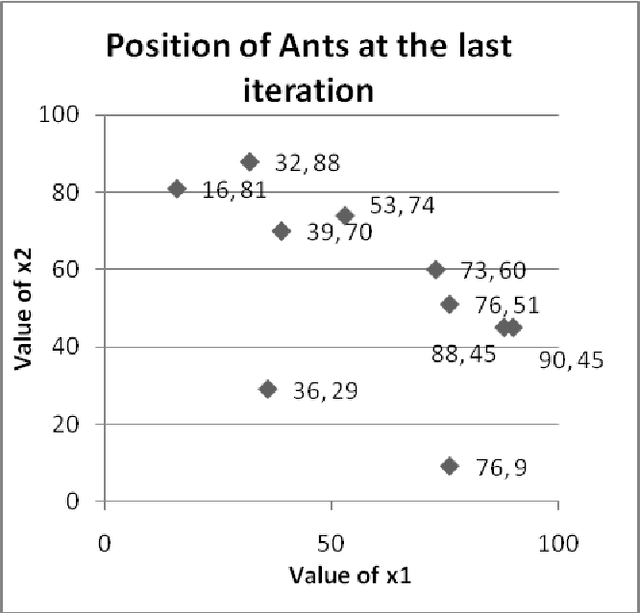
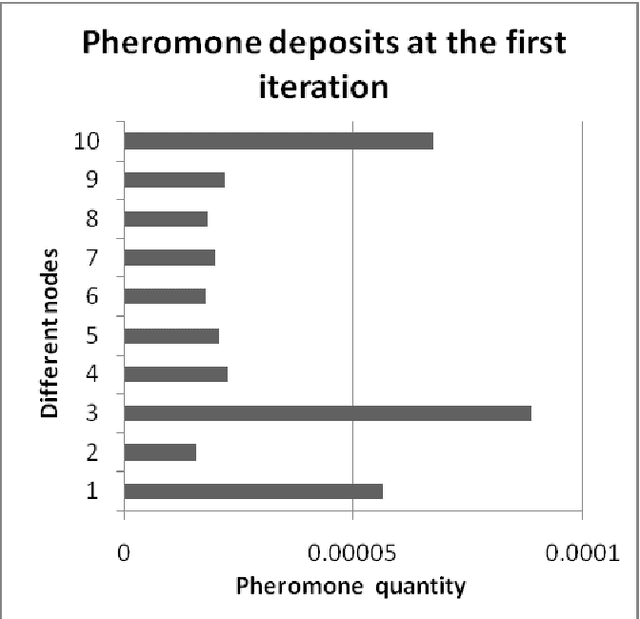
The paper attempts to find numerical solutions of Diophantine equations, a challenging problem as there are no general methods to find solutions of such equations. It uses the metaphor of foraging habits of real ants. The ant colony optimization based procedure starts with randomly assigned locations to a fixed number of artificial ants. Depending upon the quality of these positions, ants deposit pheromone at the nodes. A successor node is selected from the topological neighborhood of each of the nodes based on this stochastic pheromone deposit. If an ant bumps into an already encountered node, the pheromone is updated correspondingly. A suitably defined pheromone evaporation strategy guarantees that premature convergence does not take place. The experimental results, which compares with those of other machine intelligence techniques, validate the effectiveness of the proposed method.

A Connectionist Network Approach to Find Numerical Solutions of Diophantine Equations

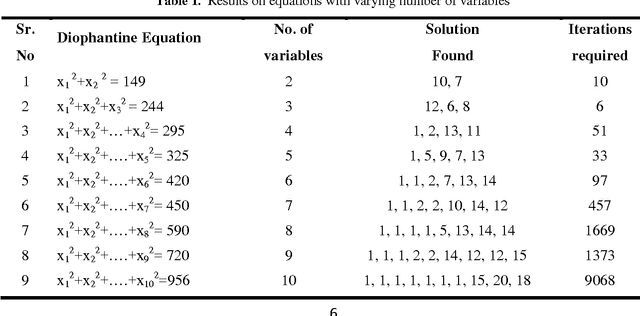
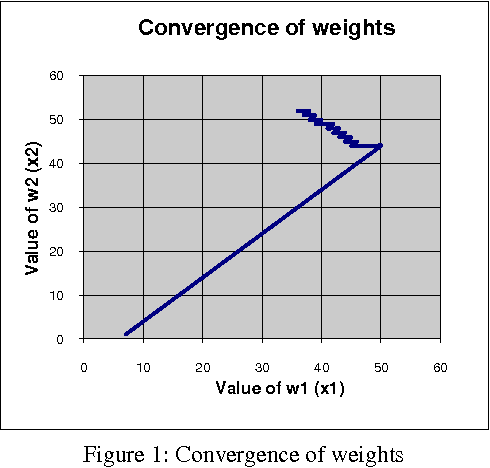
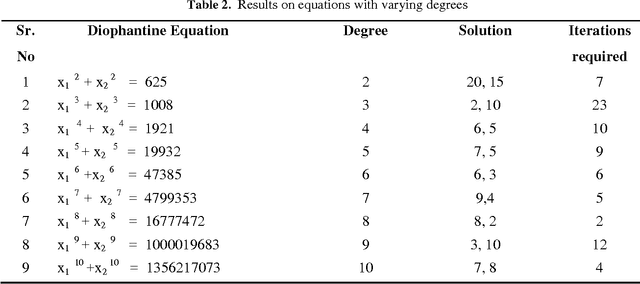
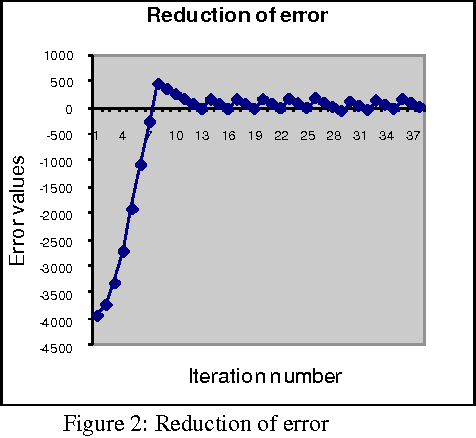
The paper introduces a connectionist network approach to find numerical solutions of Diophantine equations as an attempt to address the famous Hilbert's tenth problem. The proposed methodology uses a three layer feed forward neural network with back propagation as sequential learning procedure to find numerical solutions of a class of Diophantine equations. It uses a dynamically constructed network architecture where number of nodes in the input layer is chosen based on the number of variables in the equation. The powers of the given Diophantine equation are taken as input to the input layer. The training of the network starts with initial random integral weights. The weights are updated based on the back propagation of the error values at the output layer. The optimization of weights is augmented by adding a momentum factor into the network. The optimized weights of the connection between the input layer and the hidden layer are taken as numerical solution of the given Diophantine equation. The procedure is validated using different Diophantine Equations of different number of variables and different powers.

Steepest Ascent Hill Climbing For A Mathematical Problem

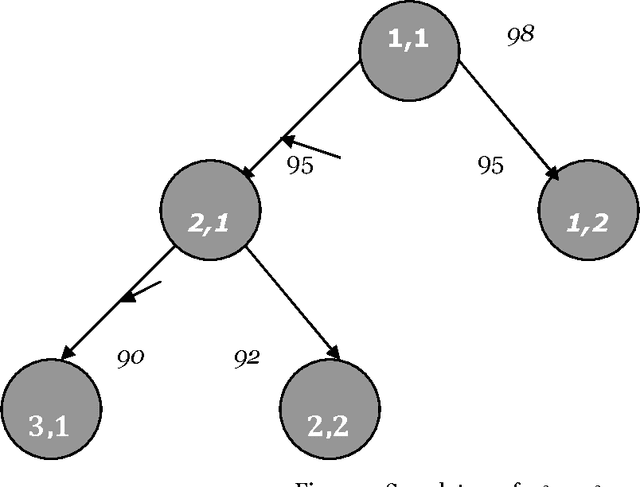
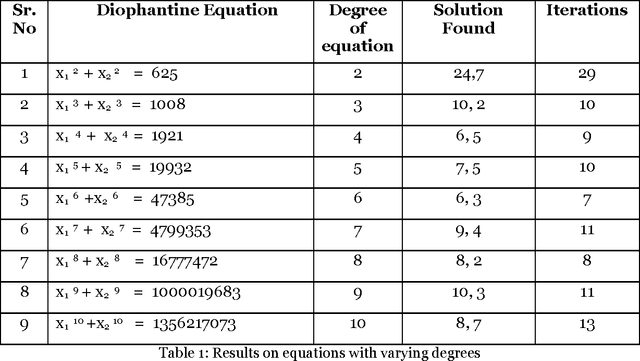
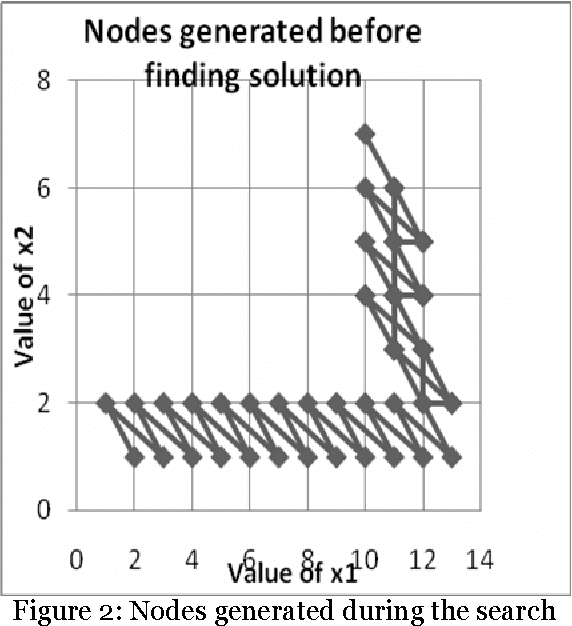
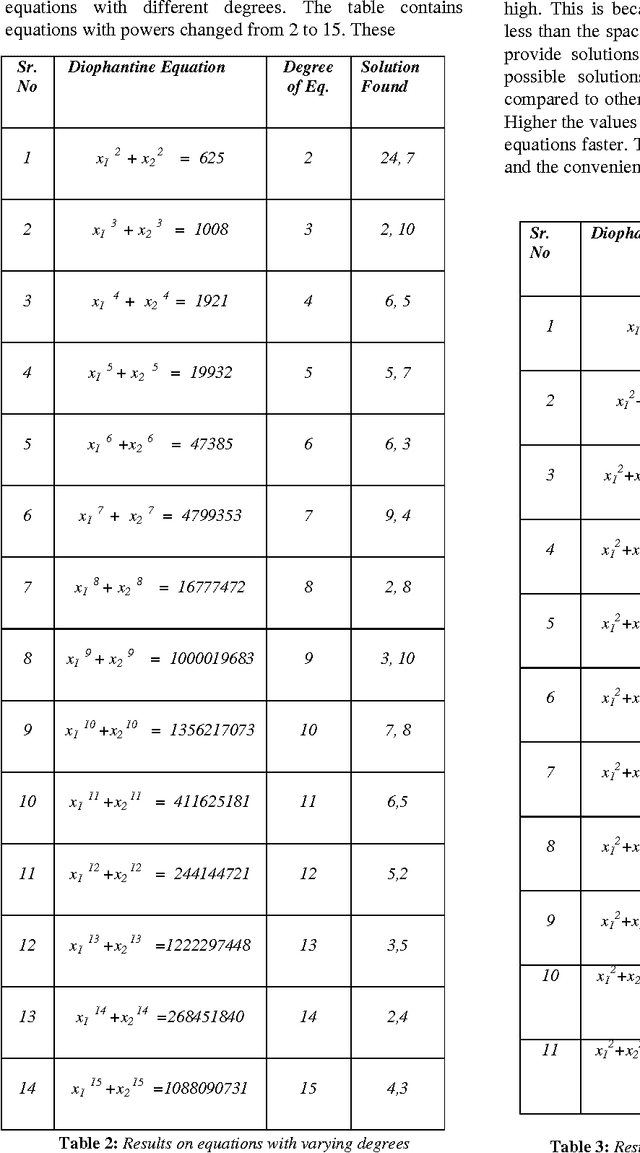
The paper proposes artificial intelligence technique called hill climbing to find numerical solutions of Diophantine Equations. Such equations are important as they have many applications in fields like public key cryptography, integer factorization, algebraic curves, projective curves and data dependency in super computers. Importantly, it has been proved that there is no general method to find solutions of such equations. This paper is an attempt to find numerical solutions of Diophantine equations using steepest ascent version of Hill Climbing. The method, which uses tree representation to depict possible solutions of Diophantine equations, adopts a novel methodology to generate successors. The heuristic function used help to make the process of finding solution as a minimization process. The work illustrates the effectiveness of the proposed methodology using a class of Diophantine equations given by a1. x1 p1 + a2. x2 p2 + ...... + an . xn pn = N where ai and N are integers. The experimental results validate that the procedure proposed is successful in finding solutions of Diophantine Equations with sufficiently large powers and large number of variables.

Particle Swarm Optimization Based Diophantine Equation Solver

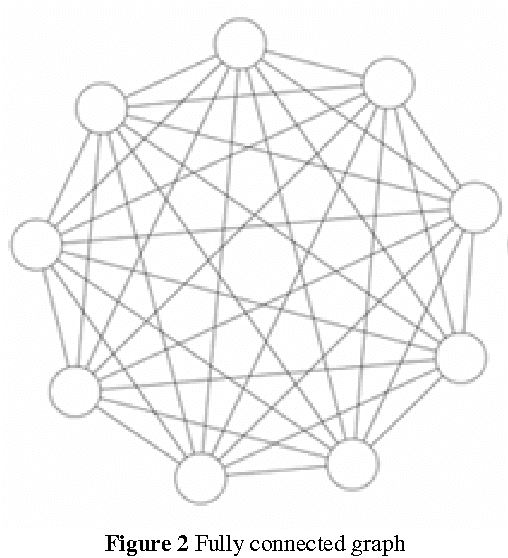
The paper introduces particle swarm optimization as a viable strategy to find numerical solution of Diophantine equation, for which there exists no general method of finding solutions. The proposed methodology uses a population of integer particles. The candidate solutions in the feasible space are optimized to have better positions through particle best and global best positions. The methodology, which follows fully connected neighborhood topology, can offer many solutions of such equations.