Steepest Ascent Hill Climbing For A Mathematical Problem
Paper and Code
Oct 02, 2010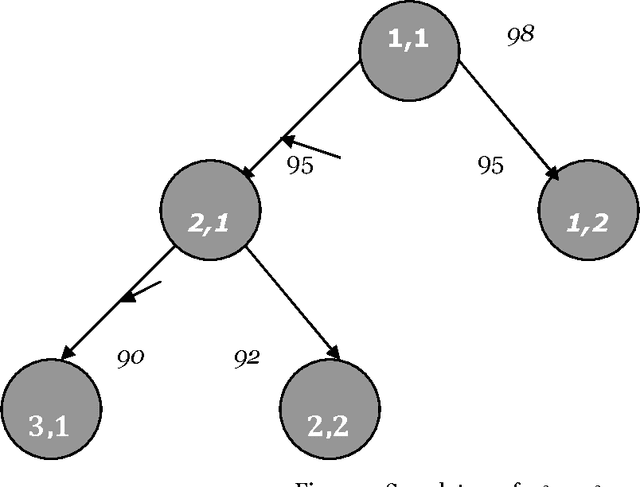
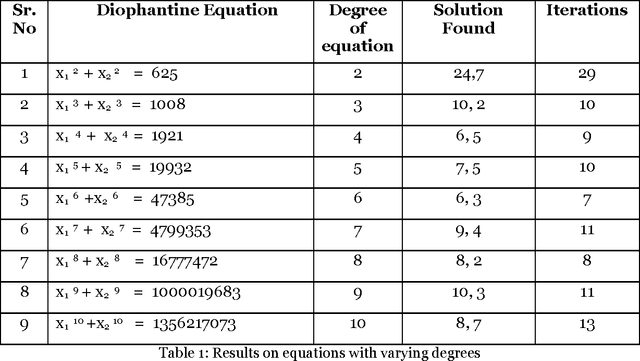
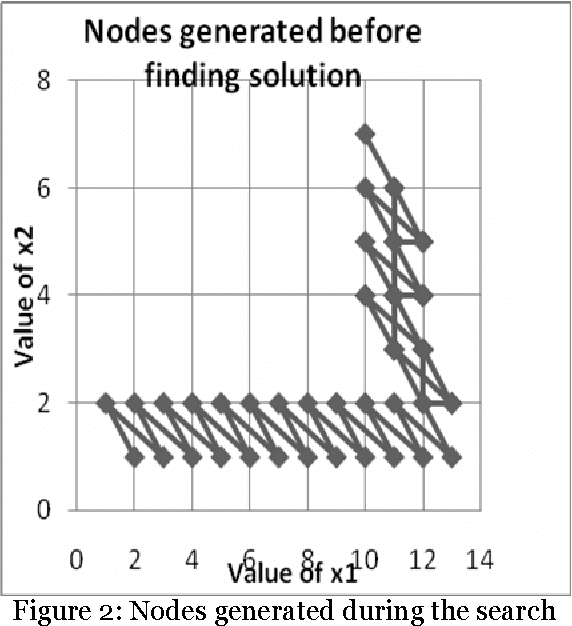

The paper proposes artificial intelligence technique called hill climbing to find numerical solutions of Diophantine Equations. Such equations are important as they have many applications in fields like public key cryptography, integer factorization, algebraic curves, projective curves and data dependency in super computers. Importantly, it has been proved that there is no general method to find solutions of such equations. This paper is an attempt to find numerical solutions of Diophantine equations using steepest ascent version of Hill Climbing. The method, which uses tree representation to depict possible solutions of Diophantine equations, adopts a novel methodology to generate successors. The heuristic function used help to make the process of finding solution as a minimization process. The work illustrates the effectiveness of the proposed methodology using a class of Diophantine equations given by a1. x1 p1 + a2. x2 p2 + ...... + an . xn pn = N where ai and N are integers. The experimental results validate that the procedure proposed is successful in finding solutions of Diophantine Equations with sufficiently large powers and large number of variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge