Motokazu Hojo
Physically-interpretable classification of network dynamics for complex collective motions
May 13, 2019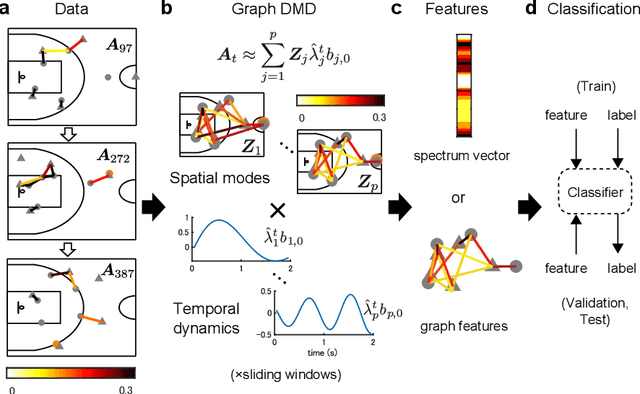
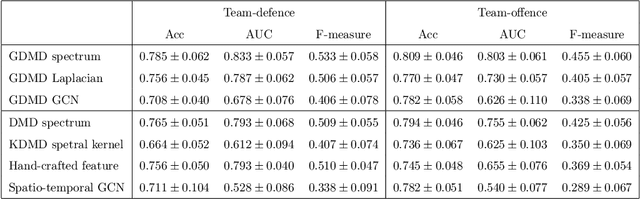
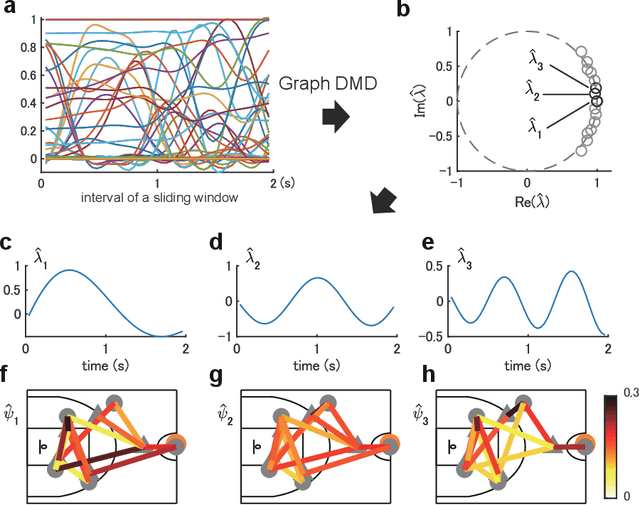
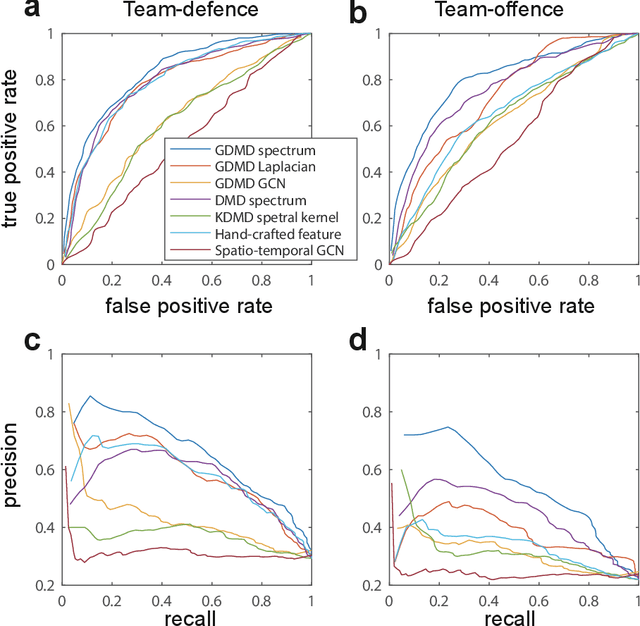
Abstract:Understanding complex network dynamics is a fundamental issue in various scientific and engineering fields. Network theory is capable of revealing the relationship between elements and their propagation; however, for complex collective motions, the network properties often transiently and complexly change. A fundamental question addressed here pertains to the classification of collective motion network based on physically-interpretable dynamical properties. Here we apply a data-driven spectral analysis called graph dynamic mode decomposition, which obtains the dynamical properties for collective motion classification. Using a ballgame as an example, we classified the strategic collective motions in different global behaviours and discovered that, in addition to the physical properties, the contextual node information was critical for classification. Furthermore, we discovered the label-specific stronger spectra in the relationship among the nearest agents, providing physical and semantic interpretations. Our approach contributes to the understanding of complex networks involving collective motions from the perspective of nonlinear dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge