Most ReLU Networks Admit Identifiable Parameters

We study the realization map of deep ReLU networks, focusing on when a function determines its parameters up to scaling and permutation. To analyze hidden redundancies beyond these standard symmetries, we introduce a framework based on weighted polyhedral complexes. Our main result shows that for every architecture whose input and hidden layers have width at least two, there exists an open set of identifiable parameters. This implies that the functional dimension of every such architecture is exactly the number of parameters minus the number of hidden neurons. We further show that minimal functional representations can still have non-trivial parameter redundancies. Finally, we establish a generic depth hierarchy, whereby for an open set of parameters the realized function cannot be represented generically by any shallower network.

On the expressivity of sparse maxout networks

We study the expressivity of sparse maxout networks, where each neuron takes a fixed number of inputs from the previous layer and employs a, possibly multi-argument, maxout activation. This setting captures key characteristics of convolutional or graph neural networks. We establish a duality between functions computable by such networks and a class of virtual polytopes, linking their geometry to questions of network expressivity. In particular, we derive a tight bound on the dimension of the associated polytopes, which serves as the central tool for our analysis. Building on this, we construct a sequence of depth hierarchies. While sufficiently deep sparse maxout networks are universal, we prove that if the required depth is not reached, width alone cannot compensate for the sparsity of a fixed indegree constraint.

Depth-Bounds for Neural Networks via the Braid Arrangement

We contribute towards resolving the open question of how many hidden layers are required in ReLU networks for exactly representing all continuous and piecewise linear functions on $\mathbb{R}^d$. While the question has been resolved in special cases, the best known lower bound in general is still 2. We focus on neural networks that are compatible with certain polyhedral complexes, more precisely with the braid fan. For such neural networks, we prove a non-constant lower bound of $\Omega(\log\log d)$ hidden layers required to exactly represent the maximum of $d$ numbers. Additionally, under our assumption, we provide a combinatorial proof that 3 hidden layers are necessary to compute the maximum of 5 numbers; this had only been verified with an excessive computation so far. Finally, we show that a natural generalization of the best known upper bound to maxout networks is not tight, by demonstrating that a rank-3 maxout layer followed by a rank-2 maxout layer is sufficient to represent the maximum of 7 numbers.

Decomposition Polyhedra of Piecewise Linear Functions

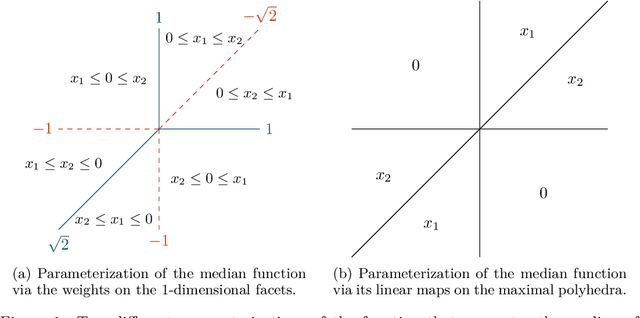
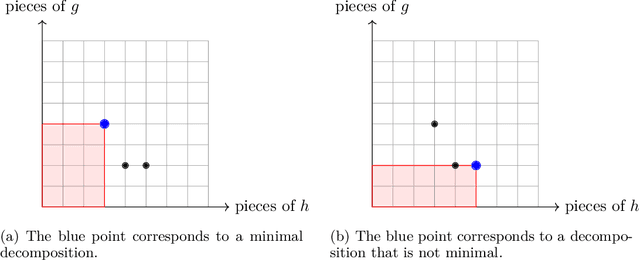
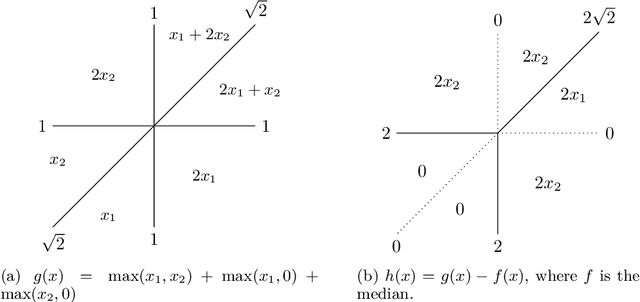
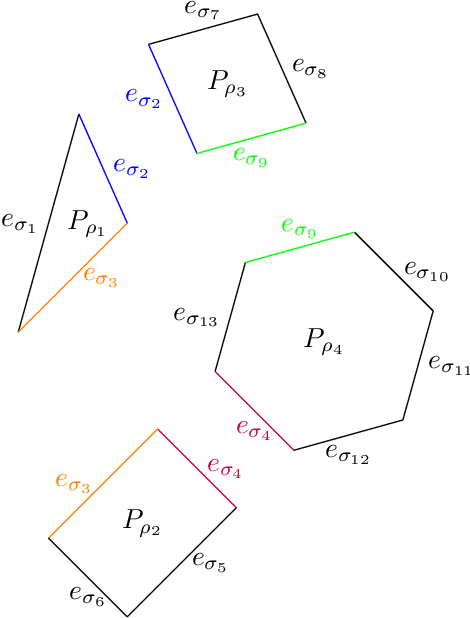
In this paper we contribute to the frequently studied question of how to decompose a continuous piecewise linear (CPWL) function into a difference of two convex CPWL functions. Every CPWL function has infinitely many such decompositions, but for applications in optimization and neural network theory, it is crucial to find decompositions with as few linear pieces as possible. This is a highly challenging problem, as we further demonstrate by disproving a recently proposed approach by Tran and Wang [Minimal representations of tropical rational functions. Algebraic Statistics, 15(1):27-59, 2024]. To make the problem more tractable, we propose to fix an underlying polyhedral complex determining the possible locus of nonlinearity. Under this assumption, we prove that the set of decompositions forms a polyhedron that arises as intersection of two translated cones. We prove that irreducible decompositions correspond to the bounded faces of this polyhedron and minimal solutions must be vertices. We then identify cases with a unique minimal decomposition, and illustrate how our insights have consequences in the theory of submodular functions. Finally, we improve upon previous constructions of neural networks for a given convex CPWL function and apply our framework to obtain results in the nonconvex case.

Complexity of Deciding Injectivity and Surjectivity of ReLU Neural Networks

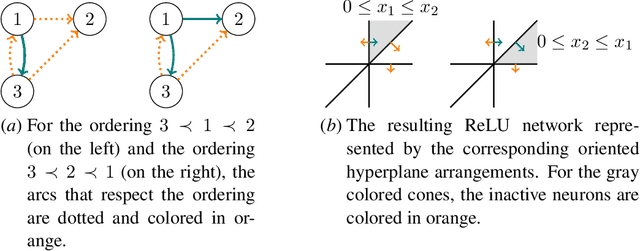
Neural networks with ReLU activation play a key role in modern machine learning. In view of safety-critical applications, the verification of trained networks is of great importance and necessitates a thorough understanding of essential properties of the function computed by a ReLU network, including characteristics like injectivity and surjectivity. Recently, Puthawala et al. [JMLR 2022] came up with a characterization for injectivity of a ReLU layer, which implies an exponential time algorithm. However, the exact computational complexity of deciding injectivity remained open. We answer this question by proving coNP-completeness of deciding injectivity of a ReLU layer. On the positive side, as our main result, we present a parameterized algorithm which yields fixed-parameter tractability of the problem with respect to the input dimension. In addition, we also characterize surjectivity for two-layer ReLU networks with one-dimensional output. Remarkably, the decision problem turns out to be the complement of a basic network verification task. We prove NP-hardness for surjectivity, implying a stronger hardness result than previously known for the network verification problem. Finally, we reveal interesting connections to computational convexity by formulating the surjectivity problem as a zonotope containment problem

Topological Expressivity of ReLU Neural Networks

We study the expressivity of ReLU neural networks in the setting of a binary classification problem from a topological perspective. Recently, empirical studies showed that neural networks operate by changing topology, transforming a topologically complicated data set into a topologically simpler one as it passes through the layers. This topological simplification has been measured by Betti numbers, which are algebraic invariants of a topological space. We use the same measure to establish lower and upper bounds on the topological simplification a ReLU neural network can achieve with a given architecture. We therefore contribute to a better understanding of the expressivity of ReLU neural networks in the context of binary classification problems by shedding light on their ability to capture the underlying topological structure of the data. In particular the results show that deep ReLU neural networks are exponentially more powerful than shallow ones in terms of topological simplification. This provides a mathematically rigorous explanation why deeper networks are better equipped to handle complex and topologically rich datasets.