How to Learn a Star: Binary Classification with Starshaped Polyhedral Sets

We consider binary classification restricted to a class of continuous piecewise linear functions whose decision boundaries are (possibly nonconvex) starshaped polyhedral sets, supported on a fixed polyhedral simplicial fan. We investigate the expressivity of these function classes and describe the combinatorial and geometric structure of the loss landscape, most prominently the sublevel sets, for two loss-functions: the 0/1-loss (discrete loss) and an exponential loss function. In particular, we give explicit bounds on the VC dimension of this model, and concretely describe the sublevel sets of the discrete loss as chambers in a hyperplane arrangement. For the exponential loss, we give sufficient conditions for the optimum to be unique, and describe the geometry of the optimum when varying the rate parameter of the underlying exponential probability distribution.

Decomposition Polyhedra of Piecewise Linear Functions

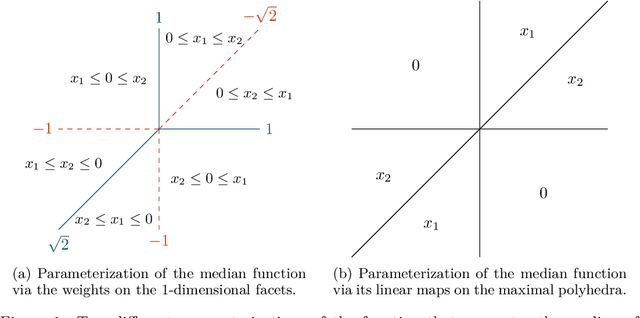
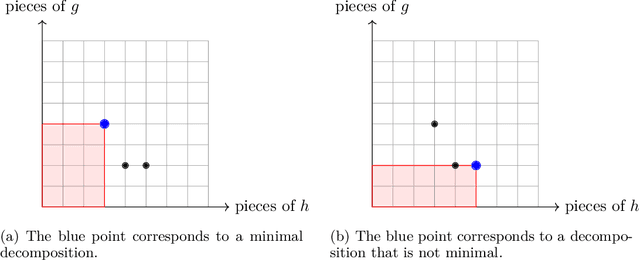
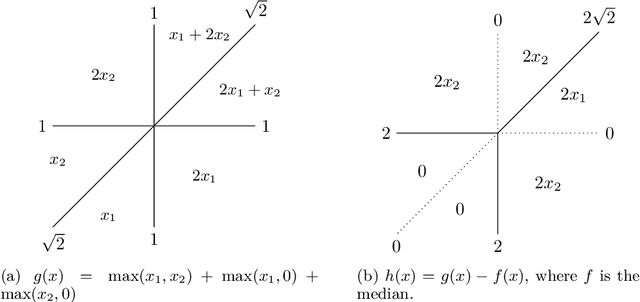
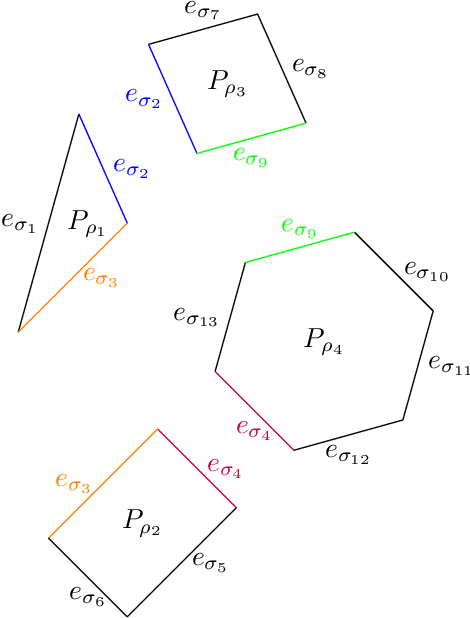
In this paper we contribute to the frequently studied question of how to decompose a continuous piecewise linear (CPWL) function into a difference of two convex CPWL functions. Every CPWL function has infinitely many such decompositions, but for applications in optimization and neural network theory, it is crucial to find decompositions with as few linear pieces as possible. This is a highly challenging problem, as we further demonstrate by disproving a recently proposed approach by Tran and Wang [Minimal representations of tropical rational functions. Algebraic Statistics, 15(1):27-59, 2024]. To make the problem more tractable, we propose to fix an underlying polyhedral complex determining the possible locus of nonlinearity. Under this assumption, we prove that the set of decompositions forms a polyhedron that arises as intersection of two translated cones. We prove that irreducible decompositions correspond to the bounded faces of this polyhedron and minimal solutions must be vertices. We then identify cases with a unique minimal decomposition, and illustrate how our insights have consequences in the theory of submodular functions. Finally, we improve upon previous constructions of neural networks for a given convex CPWL function and apply our framework to obtain results in the nonconvex case.

The Real Tropical Geometry of Neural Networks

We consider a binary classifier defined as the sign of a tropical rational function, that is, as the difference of two convex piecewise linear functions. The parameter space of ReLU neural networks is contained as a semialgebraic set inside the parameter space of tropical rational functions. We initiate the study of two different subdivisions of this parameter space: a subdivision into semialgebraic sets, on which the combinatorial type of the decision boundary is fixed, and a subdivision into a polyhedral fan, capturing the combinatorics of the partitions of the dataset. The sublevel sets of the 0/1-loss function arise as subfans of this classification fan, and we show that the level-sets are not necessarily connected. We describe the classification fan i) geometrically, as normal fan of the activation polytope, and ii) combinatorially through a list of properties of associated bipartite graphs, in analogy to covector axioms of oriented matroids and tropical oriented matroids. Our findings extend and refine the connection between neural networks and tropical geometry by observing structures established in real tropical geometry, such as positive tropicalizations of hypersurfaces and tropical semialgebraic sets.