Complexity of Deciding Injectivity and Surjectivity of ReLU Neural Networks

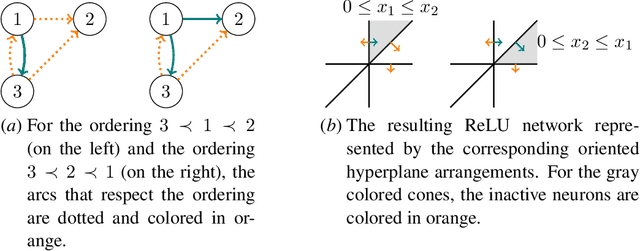
Neural networks with ReLU activation play a key role in modern machine learning. In view of safety-critical applications, the verification of trained networks is of great importance and necessitates a thorough understanding of essential properties of the function computed by a ReLU network, including characteristics like injectivity and surjectivity. Recently, Puthawala et al. [JMLR 2022] came up with a characterization for injectivity of a ReLU layer, which implies an exponential time algorithm. However, the exact computational complexity of deciding injectivity remained open. We answer this question by proving coNP-completeness of deciding injectivity of a ReLU layer. On the positive side, as our main result, we present a parameterized algorithm which yields fixed-parameter tractability of the problem with respect to the input dimension. In addition, we also characterize surjectivity for two-layer ReLU networks with one-dimensional output. Remarkably, the decision problem turns out to be the complement of a basic network verification task. We prove NP-hardness for surjectivity, implying a stronger hardness result than previously known for the network verification problem. Finally, we reveal interesting connections to computational convexity by formulating the surjectivity problem as a zonotope containment problem

Towards Lower Bounds on the Depth of ReLU Neural Networks

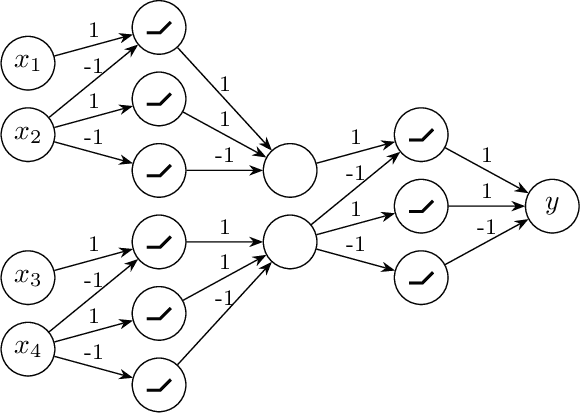
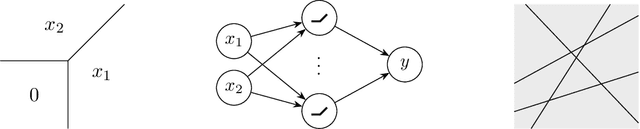
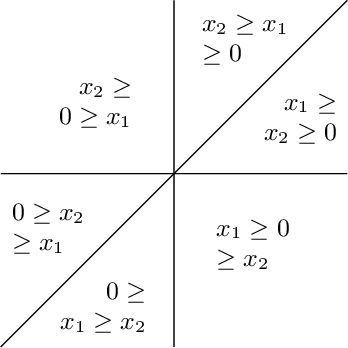
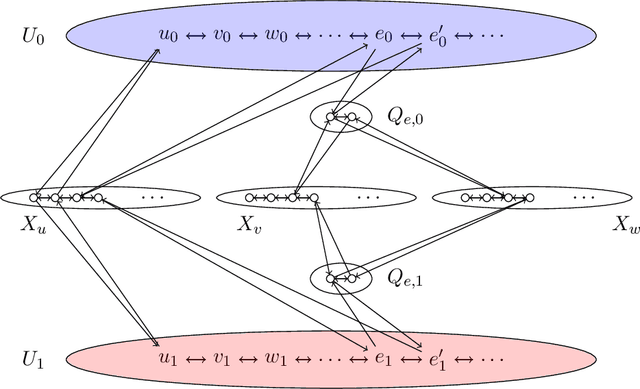
We contribute to a better understanding of the class of functions that is represented by a neural network with ReLU activations and a given architecture. Using techniques from mixed-integer optimization, polyhedral theory, and tropical geometry, we provide a mathematical counterbalance to the universal approximation theorems which suggest that a single hidden layer is sufficient for learning tasks. In particular, we investigate whether the class of exactly representable functions strictly increases by adding more layers (with no restrictions on size). This problem has potential impact on algorithmic and statistical aspects because of the insight it provides into the class of functions represented by neural hypothesis classes. However, to the best of our knowledge, this question has not been investigated in the neural network literature. We also present upper bounds on the sizes of neural networks required to represent functions in these neural hypothesis classes.

Provably Good Solutions to the Knapsack Problem via Neural Networks of Bounded Size

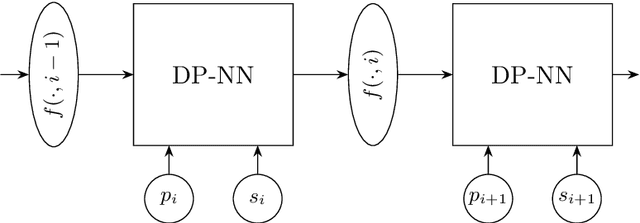
In view of the undisputed success of neural networks and due to the remarkable recent improvements in their ability to solve a huge variety of practical problems, the development of a satisfying and rigorous mathematical understanding of their performance is one of the main challenges in the field of learning theory. Against this background, we study the expressive power of neural networks through the example of the classical NP-hard Knapsack Problem. Our main contribution is a class of recurrent neural networks (RNNs) with rectified linear units that are iteratively applied to each item of a Knapsack instance and thereby compute optimal or provably good solution values. In order to find optimum Knapsack solutions, an RNN of depth four and width depending quadratically on the profit of an optimum Knapsack solution is sufficient. We also prove the following tradeoff between the size of an RNN and the quality of the computed Knapsack solution: For Knapsack instances consisting of $n$ items, an RNN of depth five and width $w$ computes a solution of value at least $1-\mathcal{O}(n^2/\sqrt{w})$ times the optimum solution value. Our results build upon a dynamic programming formulation of the Knapsack Problem as well as a careful rounding of profit values that is also at the core of the well-known fully polynomial-time approximation scheme for the Knapsack Problem. Finally, we point out that similar results can be achieved for other optimization problems that can be solved by dynamic programming, such as, e.g., various Shortest Path Problems and the Longest Common Subsequence Problem.