Towards Lower Bounds on the Depth of ReLU Neural Networks
Paper and Code
May 31, 2021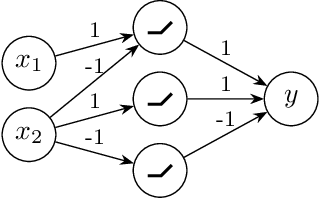
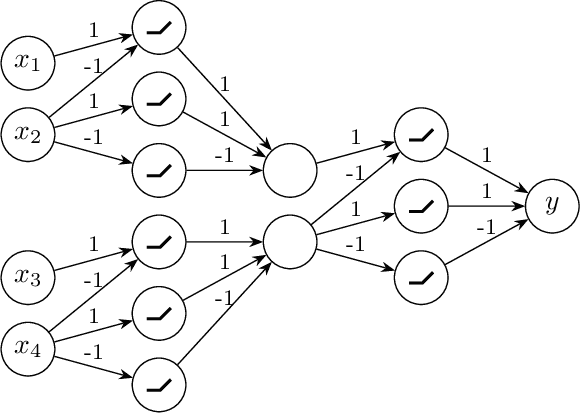
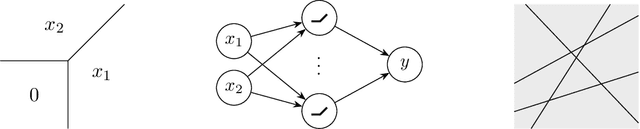
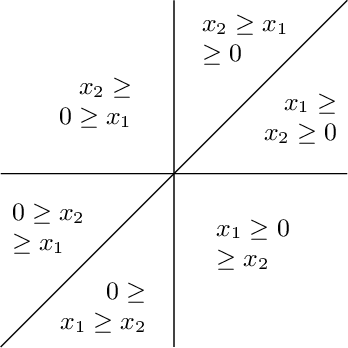
We contribute to a better understanding of the class of functions that is represented by a neural network with ReLU activations and a given architecture. Using techniques from mixed-integer optimization, polyhedral theory, and tropical geometry, we provide a mathematical counterbalance to the universal approximation theorems which suggest that a single hidden layer is sufficient for learning tasks. In particular, we investigate whether the class of exactly representable functions strictly increases by adding more layers (with no restrictions on size). This problem has potential impact on algorithmic and statistical aspects because of the insight it provides into the class of functions represented by neural hypothesis classes. However, to the best of our knowledge, this question has not been investigated in the neural network literature. We also present upper bounds on the sizes of neural networks required to represent functions in these neural hypothesis classes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge