Provably Good Solutions to the Knapsack Problem via Neural Networks of Bounded Size

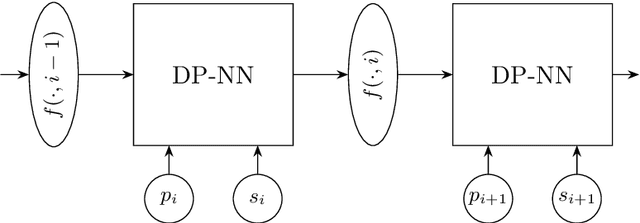
In view of the undisputed success of neural networks and due to the remarkable recent improvements in their ability to solve a huge variety of practical problems, the development of a satisfying and rigorous mathematical understanding of their performance is one of the main challenges in the field of learning theory. Against this background, we study the expressive power of neural networks through the example of the classical NP-hard Knapsack Problem. Our main contribution is a class of recurrent neural networks (RNNs) with rectified linear units that are iteratively applied to each item of a Knapsack instance and thereby compute optimal or provably good solution values. In order to find optimum Knapsack solutions, an RNN of depth four and width depending quadratically on the profit of an optimum Knapsack solution is sufficient. We also prove the following tradeoff between the size of an RNN and the quality of the computed Knapsack solution: For Knapsack instances consisting of $n$ items, an RNN of depth five and width $w$ computes a solution of value at least $1-\mathcal{O}(n^2/\sqrt{w})$ times the optimum solution value. Our results build upon a dynamic programming formulation of the Knapsack Problem as well as a careful rounding of profit values that is also at the core of the well-known fully polynomial-time approximation scheme for the Knapsack Problem. Finally, we point out that similar results can be achieved for other optimization problems that can be solved by dynamic programming, such as, e.g., various Shortest Path Problems and the Longest Common Subsequence Problem.