Learning Diffeomorphism for Image Registration with Time-Continuous Networks using Semigroup Regularization

Diffeomorphic image registration (DIR) is a critical task in 3D medical image analysis, aimed at finding topology preserving deformations between pairs of images. Focusing on the solution of the flow map differential equation as the diffeomorphic deformation, recent methods use discrete timesteps along with various regularization terms to penalize the negative determinant of Jacobian and impose smoothness of the solution vector field. In this paper, we propose a novel learning-based approach for diffeomorphic 3D-image registration which finds the diffeomorphisms in the time continuum with fewer regularization terms and no additional integration. As one of the fundamental properties of flow maps, we exploit the semigroup property as the only form of regularization, ensuring temporally continuous diffeomorphic flows between pairs of images. Leveraging this property, our method alleviates the need for additional regularization terms and scaling and squaring integration during both training and evaluation. To achieve time-continuous diffeomorphisms, we employ time-embedded UNets, a technique commonly utilized in diffusion models. The proposed method reveals that ensuring diffeomorphism in a continuous time interval leads to better registration results. Experimental results on two public datasets (OASIS and CANDI) demonstrate the superiority of our model over both learning-based and optimization-based methods.

Maximum Entropy Weighted Independent Set Pooling for Graph Neural Networks

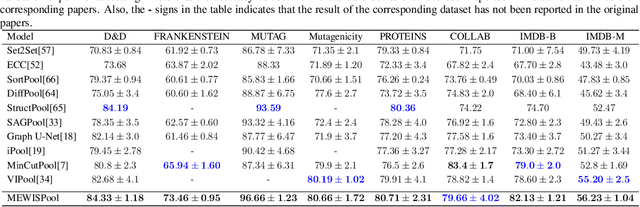
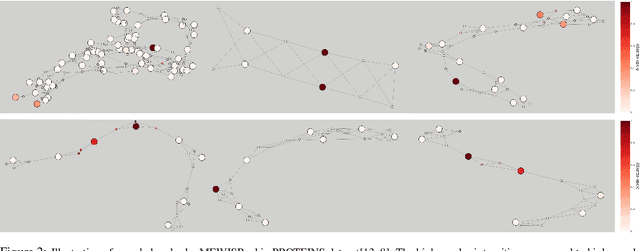
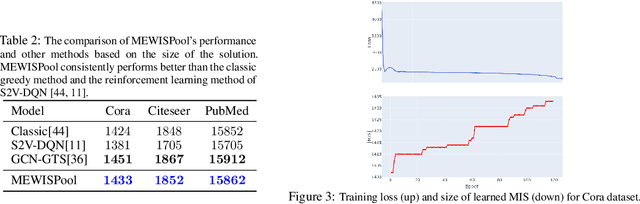
In this paper, we propose a novel pooling layer for graph neural networks based on maximizing the mutual information between the pooled graph and the input graph. Since the maximum mutual information is difficult to compute, we employ the Shannon capacity of a graph as an inductive bias to our pooling method. More precisely, we show that the input graph to the pooling layer can be viewed as a representation of a noisy communication channel. For such a channel, sending the symbols belonging to an independent set of the graph yields a reliable and error-free transmission of information. We show that reaching the maximum mutual information is equivalent to finding a maximum weight independent set of the graph where the weights convey entropy contents. Through this communication theoretic standpoint, we provide a distinct perspective for posing the problem of graph pooling as maximizing the information transmission rate across a noisy communication channel, implemented by a graph neural network. We evaluate our method, referred to as Maximum Entropy Weighted Independent Set Pooling (MEWISPool), on graph classification tasks and the combinatorial optimization problem of the maximum independent set. Empirical results demonstrate that our method achieves the state-of-the-art and competitive results on graph classification tasks and the maximum independent set problem in several benchmark datasets.