Mohammad Asghari
Epistemic Neural Networks
Jul 19, 2021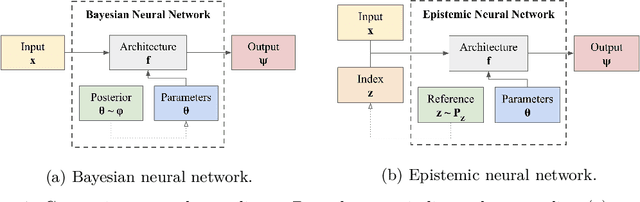
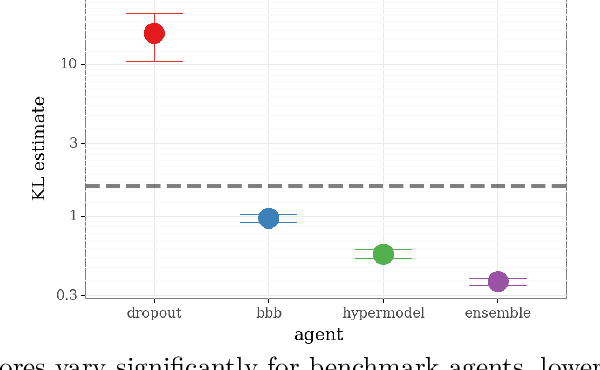
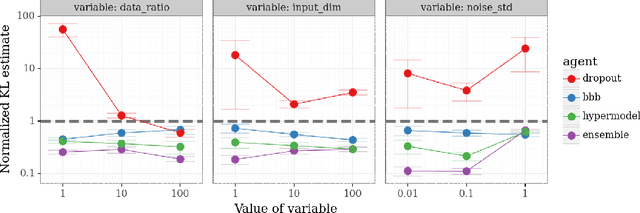
Abstract:We introduce the \textit{epistemic neural network} (ENN) as an interface for uncertainty modeling in deep learning. All existing approaches to uncertainty modeling can be expressed as ENNs, and any ENN can be identified with a Bayesian neural network. However, this new perspective provides several promising directions for future research. Where prior work has developed probabilistic inference tools for neural networks; we ask instead, `which neural networks are suitable as tools for probabilistic inference?'. We propose a clear and simple metric for progress in ENNs: the KL-divergence with respect to a target distribution. We develop a computational testbed based on inference in a neural network Gaussian process and release our code as a benchmark at \url{https://github.com/deepmind/enn}. We evaluate several canonical approaches to uncertainty modeling in deep learning, and find they vary greatly in their performance. We provide insight to the sensitivity of these results and show that our metric is highly correlated with performance in sequential decision problems. Finally, we provide indications that new ENN architectures can improve performance in both the statistical quality and computational cost.
Feature Enhancement in Visually Impaired Images
Jun 14, 2017
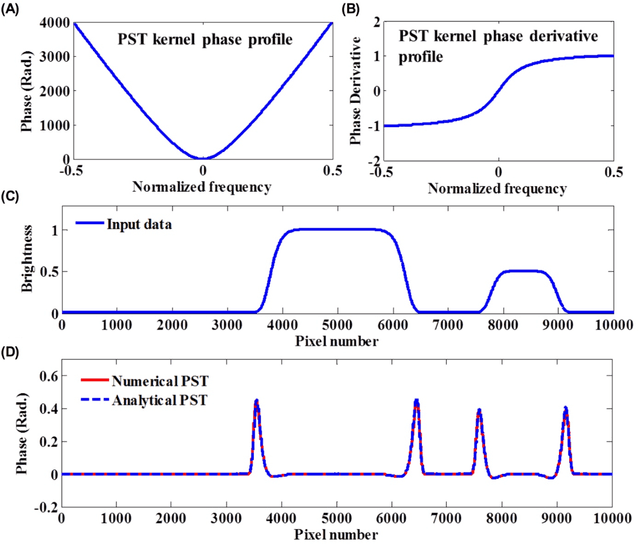


Abstract:One of the major open problems in computer vision is detection of features in visually impaired images. In this paper, we describe a potential solution using Phase Stretch Transform, a new computational approach for image analysis, edge detection and resolution enhancement that is inspired by the physics of the photonic time stretch technique. We mathematically derive the intrinsic nonlinear transfer function and demonstrate how it leads to (1) superior performance at low contrast levels and (2) a reconfigurable operator for hyper-dimensional classification. We prove that the Phase Stretch Transform equalizes the input image brightness across the range of intensities resulting in a high dynamic range in visually impaired images. We also show further improvement in the dynamic range by combining our method with the conventional techniques. Finally, our results show a method for computation of mathematical derivatives via group delay dispersion operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge