Demystifying Drug Repurposing Domain Comprehension with Knowledge Graph Embedding

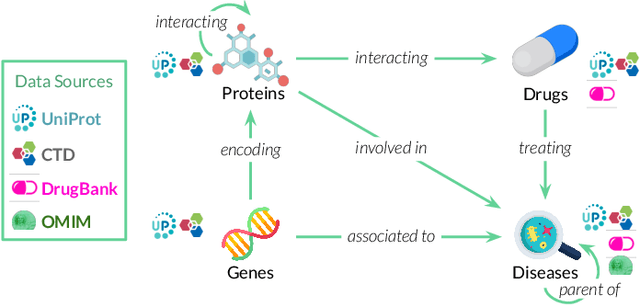
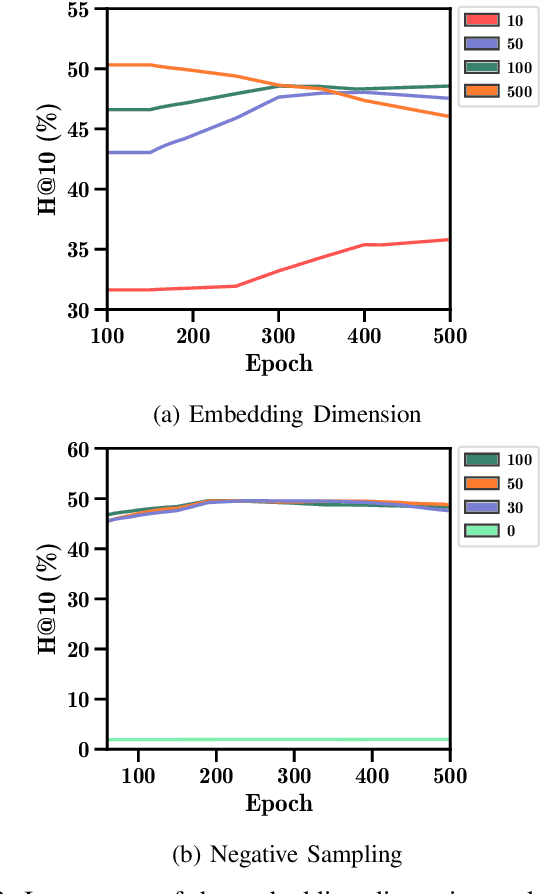
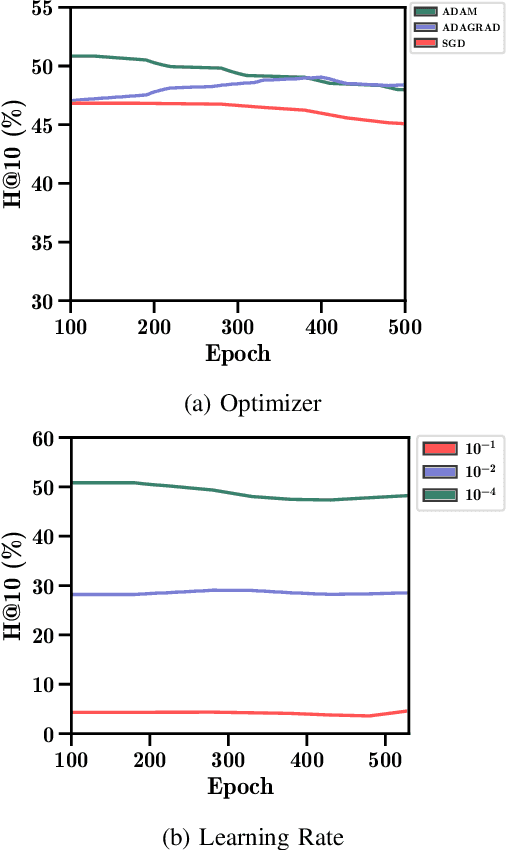
Drug repurposing is more relevant than ever due to drug development's rising costs and the need to respond to emerging diseases quickly. Knowledge graph embedding enables drug repurposing using heterogeneous data sources combined with state-of-the-art machine learning models to predict new drug-disease links in the knowledge graph. As in many machine learning applications, significant work is still required to understand the predictive models' behavior. We propose a structured methodology to understand better machine learning models' results for drug repurposing, suggesting key elements of the knowledge graph to improve predictions while saving computational resources. We reduce the training set of 11.05% and the embedding space by 31.87%, with only a 2% accuracy reduction, and increase accuracy by 60% on the open ogbl-biokg graph adding only 1.53% new triples.

Multirobot Coverage of Linear Modular Environments

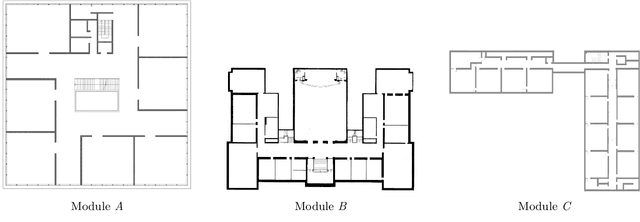
Multirobot systems for covering environments are increasingly used in applications like cleaning, industrial inspection, patrolling, and precision agriculture. The problem of covering a given environment using multiple robots can be naturally formulated and studied as a multi-Traveling Salesperson Problem (mTSP). In a mTSP, the environment is represented as a graph and the goal is to find tours (starting and ending at the same depot) for the robots in order to visit all the vertices with minimum global cost, namely the length of the longest tour. The mTSP is an NP-hard problem for which several approximation algorithms have been proposed. These algorithms usually assume generic environments, but tighter approximation bounds can be reached focusing on specific environments. In this paper, we address the case of environments composed of sub-parts, called modules, that can be reached from each other only through some linking structures. Examples are multi-floor buildings, in which the modules are the floors and the linking structures are the staircases or the elevators, and floors of large hotels or hospitals, in which the modules are the rooms and the linking structures are the corridors. We focus on linear modular environments, with the modules organized sequentially, presenting an efficient (with polynomial worst-case time complexity) algorithm that finds a solution for the mTSP whose cost is within a bounded distance from the cost of the optimal solution. The main idea of our algorithm is to allocate disjoint "blocks" of adjacent modules to the robots, in such a way that each module is covered by only one robot. We experimentally compare our algorithm against some state-of-the-art algorithms for solving mTSPs in generic environments and show that it is able to provide solutions with lower makespan and spending a computing time several orders of magnitude shorter.