Model-Free Output Feedback Stabilization via Policy Gradient Methods

Stabilizing a dynamical system is a fundamental problem that serves as a cornerstone for many complex tasks in the field of control systems. The problem becomes challenging when the system model is unknown. Among the Reinforcement Learning (RL) algorithms that have been successfully applied to solve problems pertaining to unknown linear dynamical systems, the policy gradient (PG) method stands out due to its ease of implementation and can solve the problem in a model-free manner. However, most of the existing works on PG methods for unknown linear dynamical systems assume full-state feedback. In this paper, we take a step towards model-free learning for partially observable linear dynamical systems with output feedback and focus on the fundamental stabilization problem of the system. We propose an algorithmic framework that stretches the boundary of PG methods to the problem without global convergence guarantees. We show that by leveraging zeroth-order PG update based on system trajectories and its convergence to stationary points, the proposed algorithms return a stabilizing output feedback policy for discrete-time linear dynamical systems. We also explicitly characterize the sample complexity of our algorithm and verify the effectiveness of the algorithm using numerical examples.

Output Feedback Stabilization of Linear Systems via Policy Gradient Methods

Stabilizing a dynamical system is a fundamental problem that serves as a cornerstone for many complex tasks in the field of control systems. The problem becomes challenging when the system model is unknown. Among the Reinforcement Learning (RL) algorithms that have been successfully applied to solve problems pertaining to unknown linear dynamical systems, the policy gradient (PG) method stands out due to its ease of implementation and can solve the problem in a model-free manner. However, most of the existing works on PG methods for unknown linear dynamical systems assume full-state feedback. In this paper, we take a step towards model-free learning for partially observable linear dynamical systems with output feedback and focus on the fundamental stabilization problem of the system. We propose an algorithmic framework that stretches the boundary of PG methods to the problem without global convergence guarantees. We show that by leveraging zeroth-order PG update based on system trajectories and its convergence to stationary points, the proposed algorithms return a stabilizing output feedback policy for discrete-time linear dynamical systems. We also explicitly characterize the sample complexity of our algorithm and verify the effectiveness of the algorithm using numerical examples.

Online Convex Optimization with Memory and Limited Predictions

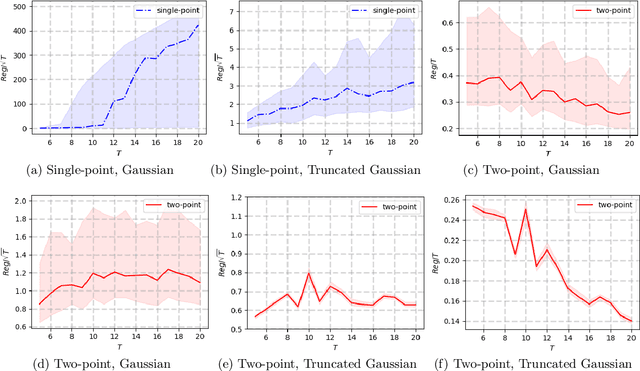
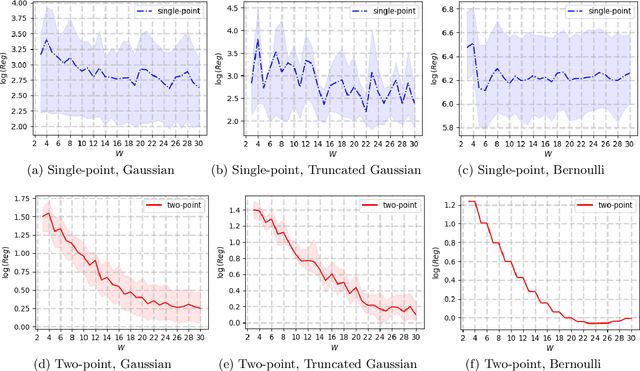
We study the problem of online convex optimization with memory and predictions over a horizon $T$. At each time step, a decision maker is given some limited predictions of the cost functions from a finite window of future time steps, i.e., values of the cost function at certain decision points in the future. The decision maker then chooses an action and incurs a cost given by a convex function that depends on the actions chosen in the past. We propose an algorithm to solve this problem and show that the dynamic regret of the algorithm decays exponentially with the prediction window length. Our algorithm contains two general subroutines that work for wider classes of problems. The first subroutine can solve general online convex optimization with memory and bandit feedback with $\sqrt{T}$-dynamic regret with respect to $T$. The second subroutine is a zeroth-order method that can be used to solve general convex optimization problems with a linear convergence rate that matches the best achievable rate of first-order methods for convex optimization. The key to our algorithm design and analysis is the use of truncated Gaussian smoothing when querying the decision points for obtaining the predictions. We complement our theoretical results using numerical experiments.

Regret Bounds for Learning Decentralized Linear Quadratic Regulator with Partially Nested Information Structure

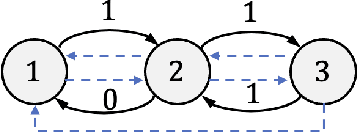
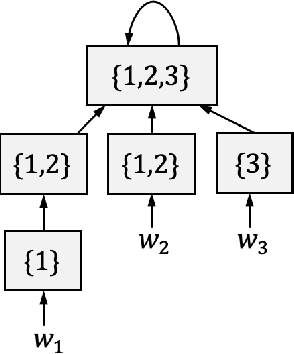
We study the problem of learning decentralized linear quadratic regulator under a partially nested information constraint, when the system model is unknown a priori. We propose an online learning algorithm that adaptively designs a control policy as new data samples from a single system trajectory become available. Our algorithm design uses a disturbance-feedback representation of state-feedback controllers coupled with online convex optimization with memory and delayed feedback. We show that our online algorithm yields a controller that satisfies the desired information constraint and enjoys an expected regret that scales as $\sqrt{T}$ with the time horizon $T$.