Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Mina GhadimiAtigh
Hyperbolic Image Segmentation
Mar 11, 2022Figures and Tables: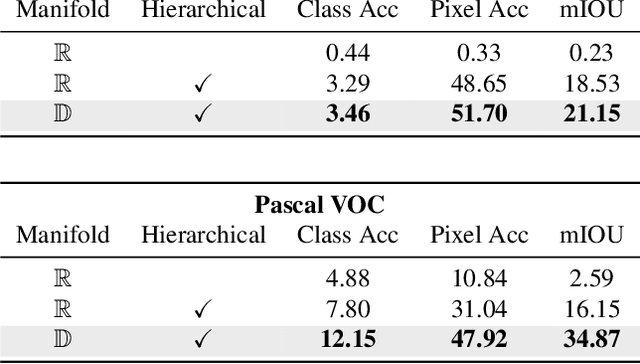
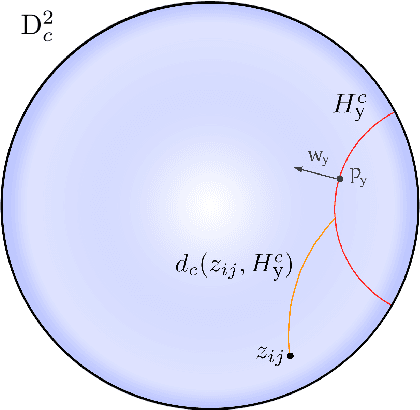
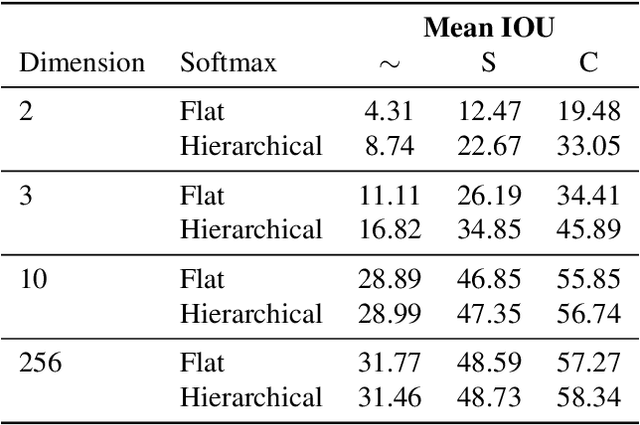
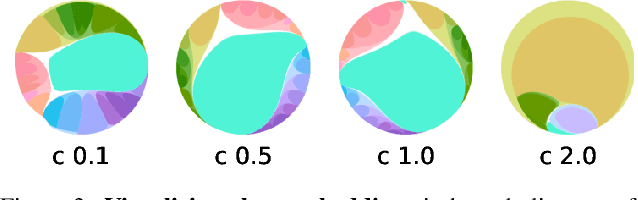



Abstract:For image segmentation, the current standard is to perform pixel-level optimization and inference in Euclidean output embedding spaces through linear hyperplanes. In this work, we show that hyperbolic manifolds provide a valuable alternative for image segmentation and propose a tractable formulation of hierarchical pixel-level classification in hyperbolic space. Hyperbolic Image Segmentation opens up new possibilities and practical benefits for segmentation, such as uncertainty estimation and boundary information for free, zero-label generalization, and increased performance in low-dimensional output embeddings.
* accepted to CVPR 2022
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge